Mathematics and Democracy

These are the slides for two lectures WDS gave at Carnergie-Mellon University, Pittsburgh PA, October 17-18 of 2006.

Warren D. Smith            Center for Range Voting       /WarrenSmithPages/homepage/works.html      (skip to lecture #2)

Abstract.
1. We argue "range voting" is the best single-winner voting method among all commonly proposed alternatives. Measurements & estimates indicate that if adopted instead of the currently most-used system, "plurality voting," humanity's lot would improve by an amount comparable to or exceeding the improvement got from switching from undemocratic forms of government to democracy. Conservative estimate: each day's delay in getting range voting costs 5000 lives.

2. We argue (by analysing an explicit political strategy to get it) range voting is, in fact, an obtainable dream.

3. We shall also discuss some other mathematical ideas for improving democracy such as the "shortest splitline" gerrymandering-abolition plan, and a low-tech plan by Ronald Rivest (as repaired by me) for fraud-proof secret ballot voting.

Speaker is mathematician who co-founded the CRV in 2005.

World situation: crises approaching. Need good decision-making.

Major incoming crises:

1. End of cheap oil,
2. Global fisheries species collapse,
3. Exhaustion of important fossil water reserves,
4. Climate change,
5. Overpopulation,
6. Nuclear and bioweapon proliferation.

Important that world make the right decisions. But what is world's decision-making algorithm?

US now sole superpower ⇒ closest simple approximation to the answer = USA's appalling voting system. Features:

• Voters can easily elect the candidate they least want (even just among the Two) thanks to "spoiler" and "cloning" pathologies.
• Rampant gerrymandering seemingly worse than most democracies;
• An elected partisan official in charge of supervising elections in 33 out of 50 states (and in other states appointed by the governor – maybe even worse);
• 98% year-ahead predictability of all important races (largest among democratic nations) and uncontested state house races about a third of the time;
• Massive two-party domination (over 99.5%) causing opposing views to be almost completely blocked out of both power and the media;
• Electoral college inspires candidates to cater only to "swing states," ignore rest;
• Highly restrictive ballot-access laws in many states designed to ensure two-party (or one-party) domination not just in office but also on the ballot. (Lieberman's run would have been illegal in 46/50 states.)

Voting systems

Systems most commonly mentioned in political science literature illustrated by example:

Plurality: A wins (most top-rank votes with 4).
Plurality+Runoff among top two: B wins over A in the runoff, 6-to-5.
Instant Runoff (IRV): C wins (eliminate E, D, F, and B in that order – doesn't matter which way you break DF tie – then C beats A in final round 7 to 4). IRV repeatedly deletes the candidate with fewest top-rank votes, then the remaining one wins.
Borda: D wins. (D's Borda score is 16+9+4+5+2=36 versus E with 12+12+6+1+3=34 and with lower scores for A, B, C, and F.) In the Borda system a candidate gets awarded 0 points if ranked last, 1 if ranked second-last, 2 if... and the candidate with the greatest score-sum ("Borda count") wins.
Condorcet: E wins. (Since E pairwise-beats each other candidate, e.g. beating A 6:5, B 6:5, C 7:4, D 6:5, and F 9:2.)
Approval Voting: If all the red candidates are "approved," then F wins with 7 approvals (versus A=4, B=5, C=3, D=6, E=5).

And with 0-99 Range Voting, it would in fact be possible to make any of the 6 candidates win, depending on how the voters chose the scores compatibly with the orderings above. In Range Voting each voter awards a score from 0 to 99 to each candidate; greatest average score wins. (Fancier rules allow also scoring a candidate with X = intentional blank = "no opinion" – only numerical scores incorporated into averages.)

Arrow impossibility theorem & Nobel causes 50 year timewaste

K.J.Arrow's (1950) theorem states that no voting method can satisfy following short list of conditions:

1. B wins? Drop C then A wins

   #voters Their Vote 8 B>C>A 6 C>A>B 5 A>B>C

   Is no dictator.
2. If every voter prefers A to B then so does group.
3. Relative positions of A and B in the group ranking depend on their relative positions in the individual rankings, but do not depend on the individual rankings of any irrelevant alternative C.

Commonly heard: "Arrow's theorem shows that no 'best' voting system exists."
"Proof": By Arrow, for every voting system, including the putative "best" system B, exists an election which makes it look bad. Construct system A which looks good in that situation. Then A is "superior" to B so B cannot be best. Q.E.D.

That all is wrong. Range voting satisfies all three criteria, accomplishing the "impossible"!

• Huh?
• Arrow's definition of "voting system" excludes range voting.
• Oh.
• True lesson of Arrow's theorem = stay away from voting systems based on rank-order ballots.
• (Reinforcement: I have a paper in which I construct "universal counterexamples" which make every voting method based on finite set of vote-types look bad [min-utility winners] while range voting [continuum infinity of vote-types] looks good [max-utility winner].)

Bogusness. "Property based" thinking misled all of political science for 50 years.

Three ways to (try to) seek a best voting system

1. Look at human elections through history, or artificial ones (paid subjects).

Pros: Real; right sample space.
Cons[Historical]: Often hard to assess how "good" different election results were or would have been and what results "would" have occurred had other election method X had been used instead. (And subjective. And you'll be accused of bias.) Also, still not really correct sample space (since space might change over time with new X...).
Cons[Paid subjects]: Very expensive. Not really real.
Cons[Both]: Little data ⇒ low statistical significance ⇒ few results. And people lie to pollsters.

2. Find planet; create eusocial lifeform that needs to conduct elections as important part of life-cycle; better decisions via the elections ⇒ more fitness; put on planet; wait 20-200 million years; see what voting system Darwinian evolution comes up with.

Pros: Real (arguably more real than with humans). Lots of data ⇒ high significance.
Cons: Spare planets unavailable in local drug store.
Pros: Already been done at least twice on this planet (social insects)!! Hundreds of trillions of very-important-to-the-insects elections so far! All voting systems considered (in some sense).

3. Measure "Bayesian regret" of different election methods via computer election sims.

Pros: Large amounts of data ⇒ statistical significance is no problem. Artificial cyber-voters better than humans: Can read their "minds" to find their true desires unpolluted by lies (measured in standard "happiness units" too).
Cons: Computer results out = only as good as the assumptions & models in. Only try voting systems you try, not all possible.
Pros: Can try large number of assumption sets & models. If so lucky that in all of them, one voting method robustly is best, convincing.
Con: If not so lucky – some methods best in this model, others best in that ⇒ bummer.

What is Bayesian Regret?

Oversimplified into nutshell: "Bayesian regret" of election method E is "expected avoidable human unhappiness" caused by using E.

More precise answer: Bayesian regret is gotten via this procedure:

1. Each voter has a personal "utility" value for the election of each candidate. (E.g., if Nixon is elected, then Jill Voter acquires -55 extra lifetime happiness units.) In computer simulation, "voters" & "candidates" are artificial, and the utility numbers are generated by some randomized "utility generator" and assigned artificially to each candidate-voter pair.
2. Now the voters vote, based both on their private utility values, and (if strategic voters) on their perception from "pre-election polls" (also generated artificially within the simulation, e.g. from a random subsample of "people") of how the other voters are going to act.
   (Note. Some people here have gotten the wrong impression that this is assuming that voters will be "honest" or that we are assuming that honest range voters will use candidate-utilities as their candidate-scores. Neither impression is correct: These assumptions are not made.)
3. Election system E elects some winning candidate W.
4. The sum over all voters V of their utility for W, is the "achieved societal utility."
5. The sum over all voters V of their utility for X, maximized over all candidates X, is the "optimum societal utility" which would have been achieved if the election system had magically chosen the societally best candidate.
6. The difference between 5 and 4 is the "Bayesian Regret" of the election system E, at least in this experiment. It might be zero, but if E was bad or if this election was unlucky for E, then it will be positive because W and X will be different candidates.

Redo steps 1-6 zillion times (i.e. do zillion simulated elections) to find average Bayesian regret of election system E.

Comments: The Bayesian regret of an election system E may differ if we

1. Vary the number of voters,
2. Vary the number of candidates,
3. Vary the kind of "utility generator" (e.g. could be based on different numbers of "issues" with different methods for generating the locations of the candidates in "issue space"),
4. Use different kinds of assumed "voter strategy", or
5. Put different amounts of "voter ignorance". (*)

∃ at least 5 different "knobs" to "turn" on our machine for measuring Bayesian Regret of elctn method E.

Results of 1999 computer simulation study:

Measured Bayesian regrets for about 30 different election methods. 720 different "knob setting" combinations tried. Amazing result: in all 720 scenarios, range voting was best (had lowest Bayesian regret, up to statistically insignificant noise). We repeat: RV best in every single one of those 720 with either honest or strategic voters, regardless of ignorance-level, #candidates (3-5), #voters (5-200), #issues (0-∞) etc.

Typical BR results table (highly abbreviated)

Warning: Table makes it appear Borda is second-best after range. But in fact the full study considers hundreds of tables like this, & in many of them, Borda is not second best, in fact in many it's way down in the rankings. The question of which system is second best has no clear answer – some better in some kinds of election situations, others in others.

A second BR study (2006)

Less ambitious (but simpler and more reproducible) study: only did the "one-dimensional 3-candidate left-middle-right" political scenario, and very few kinds of voter strategy. But attempted exhaustive set of 623700 configurations, essentially completely covering that space.

Results (some surprises):

Number of voters = 23.  Total number of scenarios = 623700.   BetterCt[][]: 
        0       1     2     3      4      5      6       7      8      9     10
      RANGE   COND  PLUR  PKING RUNOFF  BORDA APPROVAL APRNG  WORST   BEST RANDOM
 0:       0  74096 140855  97481  95160  61600  89724    348 623603      0 623354
 1:   23164      0  83007  27911  26539  19214  74446  22604 622834      0 619786
 2:   19896  13239      0  22143  11271  32453  87685  19689 616431      0 581325
 3:   22189   3246  58393      0   1197  22460  77692  21701 607990      0 597901
 4:   22301   4606  60895  14571      0  23820  79052  21805 621036      0 603912
 5:   23146  31692 114699  59603  58231      0  55232  22322 622674      0 619190
 6:   23288  58942 141949  86853  85481  27250      0  22096 622426      0 602400
 7:    1204  74380 141498  97833  95520  61620  89376      0 623606      0 623386
 8:       0      0      0      0      0      0      0      0      0      0      0
 9:   28918  79832 149525 103473 101767  67354  95336  28062 623700      0 623700
10:     328   3808  42130  25711  19664   4429  21094    296 623700      0      0

BR:   2.03    10.9  27.7   17.5   15.6   7.5    18.0   1.94   69.0     0    39.7

1. Every method (except WORST) better than every other in at least some 3CLMR situations.
2. But overall, Range voting is best method here.
3. "Gift from God": APRNG (half-honest and half-strategic range voters) actually better than either fully-honest RANGE, or fully-strategic=APPROVAL.

How much does RV matter to humanity?

1. RV=comparable improvement over democracy as invention of democracy. Both transitions non-democracy(modeled by "random winner" or better) → democracy(strategic plurality voting) → Range Voting (halfway between honest & strategic BR numbers) comparable in terms of BR reduction; if anything second looks larger.

2. Democide:

During this [the 20th] century's wars, there were some 38 million battle deaths, but almost four times more people – at least 170 million – were killed by governments for ethnic, racial, tribal, religious, or political reasons. I call this phenomenon democide, and it means that authoritarian and totalitarian governments are more deadly than war.
–R.J.Rummel (prof. Emeritus, U.Hawaii), in his book Death by Government

Rummel on his democide statistics website gives corrections now finding the democide body count during 1900-1999 to be 262,000,000, which is six times the war dead and equiv. to 7200 killed per day.

3. Government waste: Economist Martin Bailey estimates US Govt spending is 50% waste (e.g. same power military could be got with half the money, etc.); detailed tabulation in his book. That 50% is $1.1 Trillion/year, which is equivalent to 4.4 million lives per year, i.e. 12050 lives/day. (At rate of 1 life=$250,000 earned per world-average life).

4. Life expectancy & GNP/capita: Are significantly higher (on average) in democracies. (E.g: [a] Life expectancy in E.Germany jumped 6 years since reunification; [b] Taiwan 77.4 vs China 71 also 6 years; [c] Compare North with South Korea; [d] check Vanhanen's & Barro's large cross-country datasets and fits.) This leads to numbers ≈30,000 lives/day or more.

5. Saving world via better decisions: Suppose USA, by adopting range voting, lowers risk of 2-billion population crash in 50 years, by 5%. That's 5500 lives/day.

Gazillionaire donors: listen up!

Range voting gives you more "bang" for your buck than almost any other philanthropic option. Maybe the most lives saved for this small an effort. And you can be in the steep part of the learning curve by seeding the start of the RV movement, getting huge leverage for your money. (More details)

Barro's multiD least-square fit, cross-country study

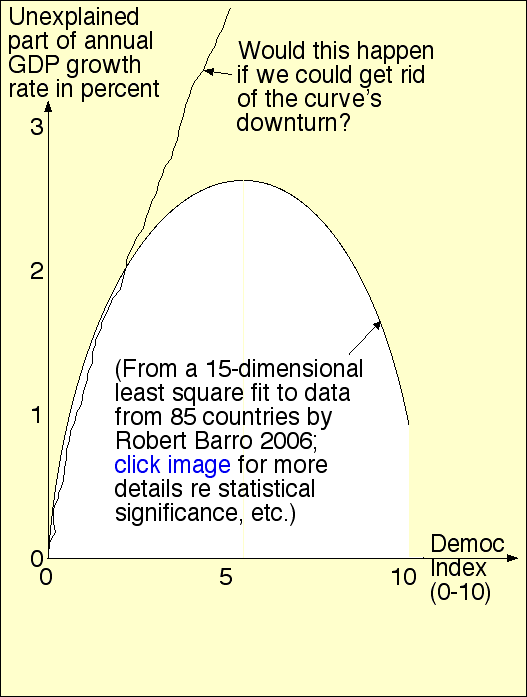
Book R.J.Barro: Determinants of Economic Growth: A Cross-Country Empirical Study predicts growth rate of country's real GDP from facts about country. GDP growth enhanced by:

• low initial per capita real GDP (then tech transfer causes fast growth; appears to be biggest effect in Barro's list)
• more secondary and higher levels of schooling,
• longer life expectancy (which presumably means good health)
• lower fertility rates,
• lower government expenditures as GDP fraction
• more "rule of law"
• favorable trade relations with other countries (e.g. the USA made trade with Cuba illegal, severely hurt Cuban economy)
• high inflation (over 20% annually) kills economic growth
• Democracy.

But democracy increases GDP in peculiar way (pictured): increases in Barro's political rights index from 0 to 5.6 on a scale of 0-10 (yielding a moderate level of freedom and democracy) increased GDP growth rates additively by 2.6% but a further increase in the index from 5.6 to 10 retarded growth by negative 1.6%.

All of Barro's causative factors (listed) cause approximately equal additive effects on predicted real-GDP-growth-rate, namely about 2-5% each. That is, having the optimum level 5.6 of political rights causes about 2.6% higher (additively) annual GDP growth rate than the pessimal level 0; countries about one standard deviation above usual in education levels are predicted to have about 3% higher than usual annual-GDP-growth; etc.

Correlation≠certainty so democracy does not force a good economy. E.g, China doing better than India.

Why that peaking and downturn?

Barro ideologically tries to explain by postulating: more democracy ⇒ more government income redistribution ⇒ hurts growth. But attackable because Barro's fit already had incorporated government expenditures as different predictor; democratization was only being fit to unexplained part of the GDP growth above and beyond that explainable as result of government outlays. Barro partly defends by saying that government transfer payments were not held constant. But, assuming Barro has idea that transfers aim toward equalizing wealth, he is exactly wrong about its economic effect: the Deininger-Squires 1998 World Bank cross-country study found that greater initial inequality is strongly negatively correlated to future economic growth!

In other words, the "trickle down theory" often associated with Ronald Reagan is wrong. According to George R. G. Clarke: More Evidence on Income Distribution and Growth, J. Development Economics 47,2 (Aug. 1995) 403-427, "This conclusion is robust across different inequality measures, and to many different specifications of the growth regression. Furthermore, inequality appears to have a negative effect on both democracies and non-democracies. Interaction terms between inequality and regime type, when included in the base regression, do not affect the sign or significance of [this]." So this seems to settle the matter. (However, to completely clarify matters, it would be good to put transfer payments into Barro's fit also, to see what happens. And two other good predictors to try inserting would be a country's winter temperature and the "centralization fraction" of its government [See A.Lijphart: Democracies 1984 table 10.2 page 178].)

Two other possible explanatory hypotheses: (more supported than Barro's):

1. More democracy ⇒ dumb people make more dumb decisions ⇒ worse economic growth.
2. Even smart people make dumb decisions if the "decision-making algorithm" is "a poor voting system." If so, then replacing voting system with better one, e.g. range voting, would yield big economic growth win, and that peak & downturn might be avoidable – the curve instead would just keep going up!

Why is RV best? (Aside from "because my computer says so.")

• Other computers say so too.
• Quick picture:
  1. RV ≈same as Approval if strategic voters & better if honest voters.
  2. RV way better than Borda if strategic & somewhat better if honest voters.
  3. Not initially so obvious versus Condorcet, but... (a) if enough voter honesty, then RV can avoid "tyranny of majority" surpassing Condorcet and every other usual method; (b) if strategic voters, can prove theorem that RV yields (under reasonable assmptns) the honest-voter Condorcet winner!
• More voter expressivity.
• More voter honesty.
• Good and/or mild reaction to "strategic voters."
• Immunity to candidate "cloning" and "removal."
• Immunity to "DH3 pathology" (Dark horse plus 3 rivals)

There's also psychological reasons, tactical reasons, and "secondary effects"...

Let's look into all these in a little more depth...

Some theorems saying range voting reacts mildly to strategic voting

Avoids favorite betrayal: In range voting, there is never a strategic reason to give your favorite a non-top score. (Unlike: IRV, Condorcet, Borda, Plurality, where favorite-betrayal often advisable.)

Semi-honesty: In range voting, if you know all other votes (or in a ≤3-candidate election even if you have only partial knowledge of the other votes), then there is always a strategically-optimal "semi-honest" threshold-style vote, where create a "threshold" T and give all candidates better than T score=99, all others score=0. (Unlike: IRV, Condorcet, Borda, Plurality, where it can happen that every honest & semi-honest vote is non-strategic.)

Pleasant surprise theorem: Suppose each voter chooses T=their expectation of the value of the winner. Then: the range-winner will maximize the number of voters who are "pleasantly surprised" (result exceeds expectations). That's an optimality property related to, but not identical to, minimizing Bayesian regret.

Range⇒Condorcet theorem: Suppose each chooses T somewhere between candidates C and A, where C and A are viewed as the two most likely to win. If one of C or A is an honest-voter Condorcet winner, then he will also be the range-winner. (Suggests that in practice, Condorcet cannot have much advantage over range.)

Voter Honesty (or lack thereof)

• ≈90% of people saying they'd vote Nader in 2000 voted for somebody else. [NES data.]
• 1950 Gallup poll: 38% of British voters wanted to vote Liberal but only 9% did.

Why? Strategy. Don't want to "waste vote." (⇒ all previous BR studies, with only "honest voters," are of little interest. Also all previous left out RV.)

19-voter example illustrating "Favorite Betrayal" & "Condorcet cycle." B wins under vast variety of rank-order election methods (e.g. Borda, Condorcet-LR, IRV).

But if the six N>G>B voters insincerely switch to G>N>B ("betraying their favorite" N) then the "lesser evil" G becomes the winner under all those voting systems – in their view a better election result.

This favorite-betrayal example very important because, once voters understand exaggerating their stances on the apparent-frontrunners can be necessary to prevent "greater evil"s victory, strategic voting is guaranteed, often causing "third parties" to tend to die out (since the strategic voters won't "waste their vote" on honest-favorite third-party candidates like N whom they perceive as having "no chance of winning").

Range Voting: Favorite-betrayal never strategically forced.

Expressivity – Range leads the pack – suggesting better behavior for honest voters

100-voter example election illustrates: old controversy between Borda and Condorcet (France ≈1780):

Condorcet: A should win. (A also wins under IRV voting method.) Borda: no, B should win! Who really should win? Good question.

How would range voting handle this? RV allows voters to say how much they prefer B over A (or whoever). Quantitatively. Really, Borda or Condorcet are both right – but depending on intensity-of-preference information unavailable to their voting methods, but available to range voting. So this example illustrates an advantage of range voting over both previous voting systems.

A 5-voter example. Borda totals: A=9, B=8, C=7, D=6. Reversed Approval counts: A=1, B=2, C=3, D=4! (Generalizes to N candidates.) Both Borda and Approval clueless; range voting (with extra intensity info) can do something sensible.

Cloning – bad news for Borda & Plurality

Several near-identical "clone" candidates run. Plurality voting: they split the vote and all lose. The very popularity of a view can cause its defeat! Borda voting (basically): enough clones ⇒ opposite effect ("teaming"); assured victory!

Cloning the Bores ⇒ huge advantage! Boring party can just arrange for mucho Bores to enter the race & totally Boring! Of course, Mushites could try to defeat that by intentionally lying in their votes by ranking Bores in opposite of true order, to try to cancel out the Borites and make Mush win. But this strategy causes them to be massively dishonest in their votes and risk not only a Bore-victory, but in fact a victory by the worst of the Bores! (Which would in fact happen if the Borons counterstrategized by also being dishonest in their Bore-orderings!) Crazy!

Mushites: fight by nominating own clones, Mush₁, Mush₂, Mush₃, and Mush₄, so they'll win. Bores: countersponsor more clones Bore₄, Bore₅, Bore₆. Etc. War of clone armies. All about gall, little to do with what voters actually want.

Has caused parties to intentionally aid opponents of their point of view ("helping a spoiler")! And it also has (more often) caused parties to intentionally hurt allies of their point of view!

Range Voting: clones & "vote splitting" don't matter, election result not affected. Can't manipulate the election by creating or abolishing clones.

Theorem (WDS 2007): Every reasonable(*) voting method based on rank-order votes is vulnerable either to candidate cloning or to favorite-betrayal. But range voting has neither defect.

(*) "Reasonable" = No "dictator," symmetric under candidate renaming, deterministic aside from tiebreaks which (if any) are random equally likely.

Removing an "irrelevant loser" Candidate

4 candidates and 7 voters. Start looking at situation on left.

Range Voting: Removing a loser (from all ballots & the election) never changes anything.

DH3 pathology – bad news for Borda & Condorcet

Common scenario: Whenever there are 3 rival contenders A,B,C plus one or more "dark horses" D that all agree are worthless no-hopers: In Borda & most Condorcet systems it pays for each for the 3 factions to dishonestly rank D "above" the other two rivals. (Strategic justification: Whichever faction votes honestly, guaranteed to lose the election. Condorcet systems with equal rankings allowed? Ranking D co-equal-last like A>B=C=D is not good enough strategy; only "full force" dishonesty A>D>B>C is strategic.)

But – Worst possible disaster result: if enough voters do that, D wins.

(DH3 resembles "spoiler pathology" & game of "chicken." But it's worse. And probably more common.)
Range, IRV, plurality: immune to DH3.

IRV = bad

I. IRV leads to 2-party domination (but the closely related top-2-runoff two-round system leads to ≥3 parties). (For voters too dumb to appreciate this, often they'll probably just exaggerate ("Bush is the best! Gore is the worst" out of dumbness anyhow; same effect as being smart.)

#voters Their Vote 45 B>G>N 10 G>B>N 10 G>N>B 35 N>G>B

#voters Their (new) Vote 45 B>G>N 10 G>B>N 18 G>N>B 27 N>G>B

B wins lefthand 100-voter example IRV election. (G, with the fewest top-rank votes, is eliminated in 1st round then B wins 55 to 45 over N.) Realistic scenario from voters and candidates positioned along 1-dimensional line.

At right, suppose 8 voters in bottom faction cleverly (but dishonestly) switch their top-2 preference order. Then N is eliminated in the first round, and then in the second round G wins over B 73-to-27. From those 8 voters' point of view, this was an improvement. Betraying Nader Pays in IRV. Voting Nader causes spoiler effect still in IRV.

II. In this 24-voter IRV election, A wins after C is dropped. But now suppose every voter reverses his preference order (now attempting to choose worst rather than best). In that case A still wins after B is eliminated. I.e. IRV contradicts itself; IRV's unambiguously "best" candidate A is here the same as its "worst"!

Also illustrates bizarre kind of strategic voting: Suppose 3 of the B>C>A voters reverse their votes to A>C>B (or alter them to A>B>C; that also works). Then B is eliminated whereupon C wins 13-to-11 over A. The raising of A from bottom-to-top in their vote caused A to lose – and voting maximally dishonestly as though they were suicidally trying to elect the worst candidate, was actually optimal strategy!

Also illustrates "no show paradox": If those three B>C>A voters had simply refused to vote, then C would have won (an improvement in their view). Different way of saying the same thing: these three voters' decision to cast an honest A-last vote caused A to win.

"Secondary effects"

"Primary" effect (reckoned using Bayesian regret): just who wins the election & how much utility that is. "Secondary" effects exert themselves over historical time in sequence of many elections. When these also reckoned, RV looks even better...

2-party domination: In systems where "favorite betrayal" common enough, "2-party domination" happens (third parties die out). 2PD quickly became massive (>99.5%) in the USA (plurality voting) since "idiotic to waste vote by voting Nader." 2PD also experimentally has always happened under IRV, despite moronic propaganda (Australia, Ireland). 2PD has not happened under plur+top-2-runoff. ("Duverger's laws.") 2PD might happen under Condorcet systems.

Consequent diminution of voter choice: Bush & Kerry: pro, versus all third-party canddts against: PATRIOT act, WTO, NAFTA, "war on drugs," Iraq war, subsidy-laden "farm bill," (tax cuts leading to) huge budget deficit.

One-party domination: 98% predictability in contemporary USA. (One reason is gerrymandering... by which one party can stay permanently in power even if only 25+ε% support.)

Cash: is extremely important in plurality voting, but perceived to be less so in other systems e.g. plur+top-2-runoff. Why? Need to demonstrate you are one of the top-2 "frontrunners," i.e. create illusion of winnability, otherwise not worth wasting vote on you. That's expensive. (Educating about issues: cheap.)

Media: Pays no attention to third-party views (no motivation; they're not news). Media "lapdogs" unquestioningly accept politicians' BS without much critical examination (because with 2-party and 1-party domination, politicians are in monopoly position to cut off media lifeblood; with multiparties no such info monopoly)

Lack of congressional oversight: For most of about 8 years, Democrats in Congress haven't been able to subpoena anyone.

Rubberstamped agency heads & judge appointments: In votes for court of appeals nominees, Republican Senators during the Bush administration (during majority control) produced 2703 votes for the nominee as opposed to only a single "no" vote (cast by Trent Lott against judge Roger Gregory, the first Black ever appointed to this position).

Bush appointed Joseph Allbaugh as head of FEMA in 2001, although Allbaugh had no expertise or experience handling emergencies, but rather had been then-Texas-Governor Bush's chief of staff & campaign manager for Bush-Cheney nationwide campaign. (Allbaugh had B.S. in political science from Oklahoma State University.) In 2003, Allbaugh replaced by Michael D. Brown – Former estate and family lawyer and bar examiner. The Boston Herald reports that Brown was "fired from his last private-sector job, overseeing horse shows... after a spate of lawsuits over alleged supervision failures... `He was asked to resign,' Bill Pennington, president of the IAHA at the time, confirmed last night."

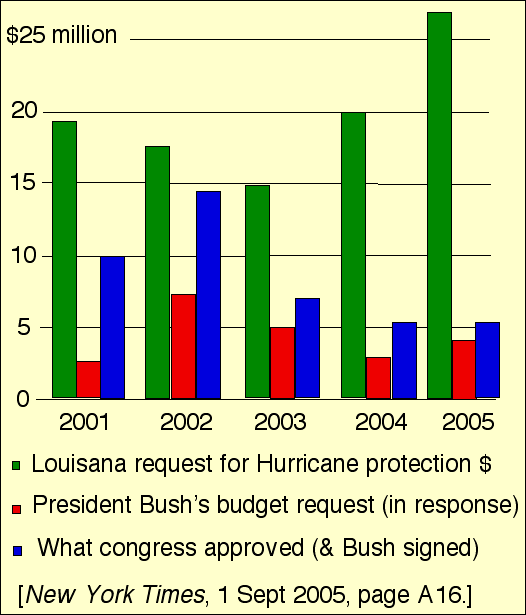
Pork & earmark game-playing:

FEMA (Federal Emergency Management Agency), in report well before both Hurricane Katrina and the 9/11 attack, summarized top 3 threats to the USA as a terrorist attack on New York, major earthquake in San Francisco and hurricane strike on New Orleans. But Bush and Congress by bipartisan budget vote turned down Louisiana's requests for mere tens of millions per year to protect New Orleans. New Orleans contained urban & poor people, many blacks, hence a high% Democrat voters; Louisiana had democrat senator, & starting in 2004, a democrat governor.

Compare with: $28 billion embassy (constructing in Iraq); $231 million for Alaska bridge between Gravina Island (population<50) & Ketchikan (pop. 8,000); Wyoming $31 million in anti-terrorism funding in 2003 (more per capita than any state).

Our exit-poll (2004 Pres. election) Range and Approval study

Pseudo-election with real US voters (122 range & 656 approval) simultaneously with the 2004 presidential election (as exit poll). Note RV psychological drive for human honesty ⇒ "nursery effect" ⇒ RV far more likely than AV to encourage growth of small third parties ⇒ enabling escape from 2-party domination, media lapdogs, rubberstamped party hack agency heads & judges, etc. Third parties: suicidally foolish to support anything besides range voting.

More data: French Approval-Voting Study and French Range-Voting Study.

1992 US Pres. Election [analysis NES data by Steven J. Brams & Samuel Merrill III Politics and Political Science 27,1 (March 1994) 39-44], the vote totals again would have been tremendously altered with approval voting (although finish order would not have changed) again illustrating tremendous distortionary penalty faced by third-party candidates under plurality system.

And in the 1980 US Presidential Election, according to analysis based on many polls in ch. 9 of Brams & Fishburn's book,

1992 results:

Candidate	Plur	AV
Clinton(Dem)	43.0	55
Bush(Rep)	37.4	49
Perot	18.9	42

Anderson probably actually would have come in second behind Reagan but ahead of Carter, under approval voting, whereas under plurality voting he was far in third place with under 7% of the votes. Again illustrates the tremendous distortionary penalty faced by third-party candidates under the undemocratic plurality system.

Psychology-aided effects

RV has some further advantages perhaps not mathematically explainable, but which instead are experimental facts that are consequences of human psychology:

1. Altruism: Range Voters exhibit unstrategic honesty to far greater degree than plurality voters. (76% of RV ballots manifestly unstrategic... versus: 90% of the time US plurality voters can choose between strategic V honest, they pick strategic.)
2. Nursery effect follows: third parties should favor RV (unless death wish)
3. Range (and approval) voters have low ballot-invalidating error rates, while IRV voters have high rates.

   Plurality: 1.0-3.1% spoiled (6 countries). IRV: 3.4-6.2% spoiled (Australia 8 territories).

   Also ≥7X increase IRV vs plurality spoilage rate in SF.

   French 2002 approval study: 2.0% spoilage for official plurality votes, 0.3% for approval exit-poll votes.

   Range: 0.026% spoilage rate (per candidate) observed in our exit poll; 99.5% confidence that range rate per canddt is at least twice as small as USA's plurality error rate of 1.8%. One reason: RV & AV: every way to fill in scores is legal. IRV & plurality: not so. Another(?): range & approval voters repeatedly do the same operation many times in each race, causing them to be more careful and inherently self-checking. (Plurality: do it only once.)
4. That'll reduce fraud-like Florida-style election manipulation.

"Spoiled ballots" & election manipulation

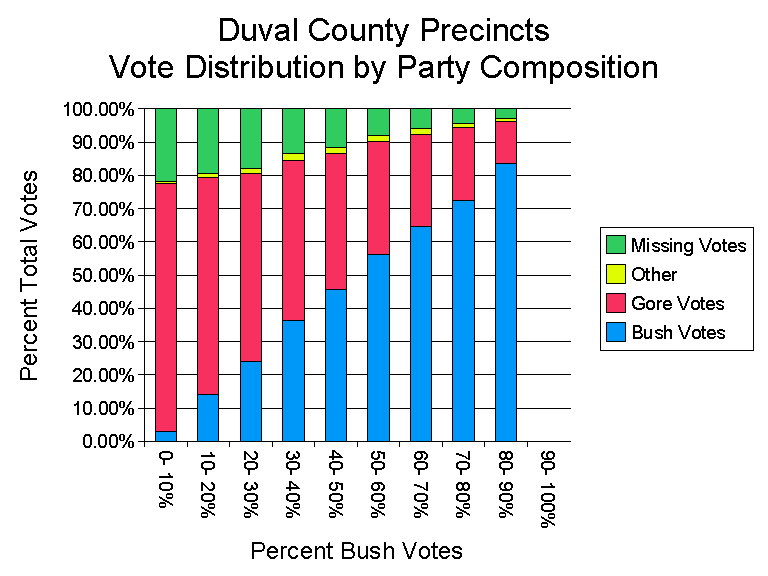
Cornell U. prof. Walter Mebane Jr. analysed ballot-level data from the NORC Florida ballots project and ballot-image files, concluded that "If the best type of vote tabulation system used in the state in 2000 – precinct-tabulated optical scan ballots – had been used statewide then [due to inequities in the distribution of voting machines & settings of those machines] Gore would have won by more than 30,000 votes." [ W.Mebane Jr.: The Wrong Man is President! Overvotes in the 2000 Presidential Election in Florida, Perspectives on Politics 2,3 (September 2004) 525-535]

This happening not only at the county level, but also district by district statewide. 268 Duval precincts: fluke result due to random fluctuations? Not. Enough to swing the Bush-Gore election result in Florida (which was decided by an official margin of only 537 votes)? Easily. (Palast maps, caption)

Tactical reasons to prefer Range Voting

1. Range Voting works, simply, on every (plurality) voting machine! Demo:

Award each candidate a numerical score from 0 to 9. Advise giving your favorite candidate 9 and the worst one 0. If you intentionally wish to express no opinion about that candidate, then please do not select any score for him – equivalently leave the default "X" choice selected; only numerical scores will be incorporated into the averaging.

Also try zohopolls, or this instant runoff demo (IRV will not run on many of today's voting machines).

2. Range Voting can get unified third-party support (due to Nursery effect, they'd be crazy to support anything else).

3. Iowa primaries strategy:

Iowa 2008 Pres-Primary Caucuses – perfect stage for range voting

Tactics: All major power groups want RV in Iowa (unlike usual)

1. Iowa caucuses get tremendous media attention, have tremendous impact despite small Iowa population. Mucho publicity for range voting.
2. Appears can change the rules without altering state or federal law, only Dem. & Repub. party internal procedures, central committee. Easier target.
3. Iowa caucuses use pen & paper ballots & manual totaling (hand calculators or adding machines). Hence can easily institute single-digit range voting – essentially no complexity penalty versus approval & plurality.
4. Both the Dems & Repubs (at all levels: rank-and-file members countrywide and Iowa-wide, Iowa state party leaders, national party leaders), are motivated to want to use range so they can get a better presidential nominee, and seem in favor of reform, and get free publicity; Iowans may also be in favor of change since many may believe Kerry (or Bush) was a mistake by them.
5. Because expect 10 Dem & 10 Repub candidates, range voting will have maximized quality advantage versus plurality & approval. Computer sims:

   "Random normal elections": How often do the range & plurality winners agree?

   #candidates:	C=2	3	4	5	8	10	15	20	50	100	200
   5123 voters	100%	73%	61%	52%	38%	32%	24%	19%	8%	4%	2%

6. Third parties want range voting and their supporters constitute at least 1% and arguably as much as 40% of society. They could swing the election. It is worth catering to their desires, especially when it also benefits everybody else including the major parties and all USA-wide.
7. Leads to voter education, reform, free good publicity beneficial for all involved, and better US presidential candidates.

Social Insects

Honeybee (Apis Mellifera) swarms (each spring) and the 3mm-long eusocial ant Leptothorax Albipennis (after nest destruction) both use range voting to decide on the location of their new nest.

Problems bees face: Tiny brains. Can they do "addition," "division," and "averaging"? If so, can they communicate results reliably? What if some bees mentally defective or miscommunicate? How to reach a swarm-wide consensus? How to do it quickly? "Robust log-time parallel algorithm"...

How bees do it:

1. Scouting. (Only 5%=scouts, rest sit there.)
2. Dances. Better nest sites get longer, more vigorous dances (greater "range vote scores").
3. More (& hotter) dancers at any given time ⇒ more probability of recruiting new scout ⇒
4. Higher "exponential growth rate" for nest sites with greater range votes.
5. Eventually the faction advocating the site with greatest average score, dominates population (even if initially small; higher exponential wins out over constant factor).
6. "Quorum rule" that it ain't over until enough votes are in.

How good are they? Swarm: 2000-20000 bees. ≥10¹⁵ elections so far. Usually find ≈20 different housing options within about 100 km², and ≈90% of the time, bee swarm succeeds in selecting (what appears to entomologists to be) best one.

Compare plurality-using humans: Computer sims ⇒ 1283 honest plurality-voters, given 10 choices (each voter regards each choice as worth standard-normal-random-number "dollar amount," all randoms generated independently before experiment begins) succeed in choosing the best (maximum ∑ dollars) 32% of the time.

Random guess: (10%),

Sim-humans employing "approval voting" (approving choices with value greater than midway between the best & worst available) then 54%.

Sim-humans employing "range voting" (scoring best choice 99, worst 0, rest linearly interpolated) then 79%... at least approaching bee-quality.

Ants: The most successful macroscopic land animals (15-20% of all land animal biomass?!). 200 Myr old.

Splitline algorithm to get rid of gerrymandering

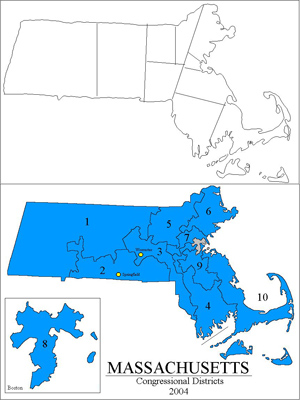Shortest splitline algorithm eliminates gerrymandering. Basically: find shortest line splitting state into two parts with right population ratios, then continue recursively. This produces better district maps for less cost than present methods and is completely unbiased. Blue map shows Massachusetts as gerrymandered to have 100% Democratic congressmen, versus districts that would have been produced by splitline.

Arizona 2004 (pdf); Texas 2003 before & after (jpg); Art gallery (gifs); Illinois 2004 (pdf); (Chicago gifs); N Florida gifs; S Florida gifs+closeups; Maryland gif as redistricted.

You want "Voter-verifiable paper trails"? Check this out.

Rivest 3ballot & BOFFO/OFF plans

(Executive Summary)   (Recipes only)   (Cheapo plan)   (Return to main page)

Abstract: Revolutionary new protocol called "3ballot" introduced September 2006 by Ron Rivest. Accomplishes seemingly incompatible goals:

1. Each voter's vote is secret, preventing vote-selling and coercion. (Even if voter wants to reveal her vote, she cannot.)
2. Each voter can verify her vote was not discarded, was correctly used and not altered, in computing election result. (And if not, voter in position to prove vote counters cheated.)
3. Everybody can verify election result computed correctly.
4. Everybody can verify that extra fake "voters" were not added; full list of voters is publically known.
5. Whole protocol can be done without computers or cryptography – only low-tech devices like paper and pens are needed – and is so simple it can be understood by children. (It is also possible to put in computers and cryptography; several flavors possible.)

Interestingly, 3ballot turns out to work most naturally, securely, and simply, for approval voting and range voting. It still works – but less naturally, securely, and simply for plurality voting (the kind of voting currently most common throughout the USA and world) – and it essentially does not work at all for voting methods based on rank-order ballots such as instant runoff voting. (There is a way to try to do it for Borda and Condorcet voting, but the resulting scheme is vulnerable to the reconstruction and and specified-pattern attacks, i.e. is a clear failure in elections with 12 or more candidates. And can't even try – 3ballot does not work at all for – Instant Runoff (IRV).)

Actually, Rivest's original plan was intended for plurality voting, but turned out not to work because it permitted vote-buying. I pointed out to Rivest, though, that (a) did work for approval and for range voting; (b) modification of his idea called "BOFFO" (simplifiable to "OFF"), works for plurality voting; (c) can also be made immune to all collusive attacks. I presume later versions will appear of the Rivest paper which will incorporate these improvements and fixes. They are, at any rate, described here.

Secure 0-9 Range Voting (do 0-1, easier, for Approval) via 3-ballot:

1. Voter decides (for some given candidate "Gladstone") what score S, on an 0-9 scale, to award Gladstone.
2. Voter submits 3 ballots about Gladstone, with scores A,B,C where A+B+C=S+9 and 0≤A≤9 and 0≤B≤9 and 0≤C≤9. Simultaneously she signs form saying "I, Jill Voter, address 57 Bogus Road, Baloney Town certify I just scored Gladstone." (And shows ID to the polling officials...)
3. Trivially simple machine (a) checks that these 3 ballots obey the 9≤A+B+C≤18 and 0≤A,B,C≤9 rules. (b) drops them into a glass-walled bin in random order, and (c) spits out a government-certified official ballot copy ("receipt") of one of the three ballots, for the voter to take home and keep in a safe place. It is important that (i) this machine be so simple – preferably not computerized – that cannot possibly be remembering the ballot-triple and (ii) it is the voter who chooses which of the three to copy.

   Worried that this might be too complicated for voters (especially Florida voters) or for a noncomputerized checking machine? Check out Jan Kok's remark.

4. Government posts all ballots in all bins onto world-readable bulletin board. For example, if you approval-voted for Gladstone, then up there on that bulletin board, somewhere, will be your 3 ballots saying "I approve Gladstone," "I approve Gladstone" , and "I disapprove Gladstone" respectively. Also posted (on another list) will be the names & addresses of all the voters who voted about Gladstone.
5. Anybody can now total the votes to find candidate with highest average score (election winner).
6. The voter can check that her vote was used in unaltered form by simply going to the bulletin board and looking up ballot number 16674568703 (Or whatever; it says number on her official copy) and comparing. [If differ, raise hell.] Note. It is important to prevent vote-buying that voter cannot remember the ballot numbers on the ballots she does not get a copy of. Hard to remember large numbers, especially if really are pixelated "bar codes." But even for voters who can remember these (or have camera) then still can achieve security by using scratch-off tricks suggested by Danny Sleator.
7. Voter can also check that her name is on the list (lookup "Jill Voter").
8. Reporters can check that the names posted on the list really are of real people who live at their addresses and who agree that they voted about Gladstone. [If not, raise hell.]

Why the talliers cannot alter your vote and cheat

Yes, an evil government could alter the two votes/scores Jill Voter cast that she does not have a certified copy of, but govt does not know which those two were – so if tries, liable to mess with the one she has copy of, enabling her to prove cheating happened. If any substantial number of votes are altered, cheat-detection essentially certain.

Why you can't sell your vote or be coerced

Because your vote secret. So vote-buyer or coercer cannot be sure you really voted the way he wanted. Even if you intentionally show vote-buyer your receipt, vote-buyer still has absolutely no idea how you really voted in total because cannot see the other parts of your vote (for which you have no receipt) – all possibilities still open. (Even if you swear a sacred oath that you voted for Bozo in those other parts, you have no way to prove it to the vote buyer. Might swear another oath to another buyer tomorrow, that you voted for Clodnik!)

Secure Plurality Voting via BOFFO (also showing how to defend against collusive attacks):

Assume N-candidate election for some N≥2.

1. Voter decides for which of the N she wishes to vote. Suppose candidate she chooses is Bozo.
2. Voter also chooses two other candidates, call them for concreteness Osbert and Foo. These could be anybody. It is also allowed for Osbert and Bozo to be same (or Osbert and Foo to be same, or all three same, or all three different).
3. Voter submits these 5 ballots:

   FOR	Bozo
   FOR	Osbert
   FOR	Foo
   AGAINST	Foo
   AGAINST	Osbert

   Simultaneously she signs form saying "I, Jill Voter, address 57 Bogus... certify I just voted." (And shows ID to the polling officials...)
4. Trivially simple machine (a) checks that these 5 ballots obey the BOFFO format rules above (i.e. there are exactly 3 FOR and 2 AGAINST votes (in some order, not necessarily the order shown) that include two FOR-AGAINST canceling-out pairs, (b) drops them into bin in random order, and (c) spits out two government-certified official ballot copies ("receipt") of either
   1. two of Jill's five ballots [she chooses which two], or
   2. one copy [she chooses which one) plus a copy of one of the ballots cast by a previous voter and randomly selected from the bin.
   Jill Voter takes these two official copies home with her for safekeeping. Which of {A,B} happens, is made randomly by flipping a coin or some other obviously random process (or could be chosen by the voter – both work, but I prefer randomness for this purpose) and is not known to anybody besides the voter and not remembered by the machine. Note: The fancy trick here of using (A) or (B) is intended for later use in protecting against collusive attacks. If we were not worried about collusive attacks, then we could just do (A) only, or even more simply, just give Jill one copy of one of her 5 ballots [she chooses which] to take home.
   It's important that (i) this machine be so simple that it cannot possibly be remembering the ballot-quintuple and (ii) it is the voter who chooses which one (or two) of the five to copy, and the machine cannot remember which one or two it was [and we can allow it to be an obviously-random device (rather than voter) which decides among possibilities A or B, but the machine must not remember that either].
5. Government posts all ballots in all bins onto world-readable bulletin board. For example, with this vote, up there on that bulletin board, somewhere, will be your 5 ballots saying "FOR Bozo", "FOR Osbert", "AGAINST Osbert" etc. Also posted (on another list) will be the names & addresses of all the voters who voted in this race.
6. Anybody can now total votes to find out candidate with the largest number of votes (election winner) where each FOR vote counts as +1 and each AGAINST vote as -1.
7. The voter can check... [as before]
8. Reporters can check... [as before]

Collusive attacks

Vote-buyers/coercers, evil vote-talliers, cannot cheat acting alone. But "3-way collusions" with vote-sellers can zap the original 3ballot scheme... (and danger: these "collusions" not as unlikely as collusions usually are...)

Nasty Collusion Scenario 1: Bush voters urged to turn in their receipts, especially "FOR Clinton" receipts (!), to Republican party officials in "watchdog" organization for "safekeeping" and "own protection". Repubs then get their hack-appointee (ala Ken Tomlinson) at elections commission to alter all those "FOR Clinton" third-votes to "FOR Bush" and burns its "FOR Clinton" receipt collection (since after all, its job is to protest about altered "FOR Bush" votes...)

Nasty Scenario 2: Receipts collected from Dumpsters used in same way.

Nasty Scenario 3: Voter just goes to corrupt govt official and says "please! fake my ballots!" and hands in her ballot receipts so they can be burned so nobody can prove the fakery happened.

Protection is afforded by the extra random copies... So Tom DeLay cannot be sure there are not other copies floating around... or that some "loyal Republican" voters not doublecrossing him...

Result: scheme with these defenses now seems also immune to all collusive attacks too (at least all the ones Rivest & I could think of...)

Closer look at why now collusion-resistant: For example, in nasty scenario #3, suppose Jill Voter hands in both her receipts to Dr.Evil (corrupt govt official) & says "please fake my vote." Well, how does Evil know that Jill was not a B-type voter, in which case one of these receipts was really of a previously cast (not by Jill) vote, in which case that previous voter may have a receipt?! So Evil can't afford to alter those votes – he'd likely be caught (and if Evil alters K votes, chance of being caught exponentially approaches 1 as K→∞). Evil cannot afford to trust Jill's word she is type-A – Jill might be an agent provocateur. Even if Jill is the first voter of the day and everybody knows it (in which case we know she is a type-A voter) then Evil still stymied – some later voter could have a Jill-vote copy. For every single vote there is a chance somebody unknown owns a copy of that vote, hence no collusive attack can work without detection.

Odds and Ends

OFF plan: Simpler than BOFFO is just OFF (Opposed, For, For = pro-O, pro-F, against-F) and (A) is "Voter gets one of her 3 ballots copied" while (B) is "Voter gets one random previously-cast [not by her] ballot copied." This also works and it is superior in the sense that 3 is simpler than 5. Only botheration is B-type OFF-voters cannot verify their own vote, which is psychologically bad compared to BOFFO where all voters can verify own vote.

OFF₂ plan: To respond to that, make simpler-still OFF plan but now each voter gets one copy of own ballot (voter chooses which) plus one random copy of a previous voter's ballot. This also works. (Note: very first voter of the day, who only gets 1 copy, could via a collusion with govt arrange to get 3 votes not 1? No, that won't work because a later voter might have a copy of her vote...)

Write-in ballots:
Rivest Approval & Range voting: no problem to do write-ins.
BOFFO/OFF Plurality voting: we must forbid write-in voting because that brings back redundant info with a vengeance.

Vote-Buyer/Coercer:	I demand you do not vote for Clinton.
BOFFO Voter:	Make me.
Coercer:	Write-in "FOR Bozo65hu636h4364", "FOR Osbert77hjkg87thh", "AGAINST Osbert77hjkg87thh", "FOR Foobar79948hj683g65", and "AGAINST Foobar79948hj683g65". I'll be checking the bulletin board later, and all those ridiculously-unique names had better be there.
Voter:	But then I won't be able to vote for Clinton!
Coercer:	(grins wolfishly) Bummer.

Borda and Condorcet voting: Michael A. Rouse invented way to do these, but it is vulnerable to specified pattern attack and is unuseable if too many candidates (e.g. if ≥12 candidates , then is insecure, but fine if only a few). And IRV (which is non-additive) does not even work at all – even if only 3 candidates. Also with Rouse's scheme, again write-ins must be forbidden.

Same anti-collusion tricks can also be added to approval & range voting 3ballot plan, of course.

Hassle: Combining both scratch-off & anticollusion tricks makes procedures pretty disgusting. For that reason the scratch-off tricks are probably not desirable in practice (?).

Randomization? Bad idea. Schemes where a random device, not the voter, select which ballot to copy, or select how to fill in the 3 (or 5) ballots for the voter, do not work; permit "statistical vote-buying." (It's about adversaries, not randomization.)

Bundling – Just say no!

Do not bundle multiple races onto one ballot. And with approval and range, do not bundle multiple candidates onto one ballot (all candidates are independently scored and should be on seperate mini-ballots). Pointless bundling enables selected-pattern attack.

Linked Numbers attack: A lot of people had ideas where there would be one ballot for the voter to fill out but then it would be cut apart into many little slips of paper, each with its own serial number pre-printed on it, and only these would be posted on the bulletin board in unbundled form. This would be more convenient for the voter and would allow bundling without worries... But that does not work!! Because the "different and unrelated" serial numbers in fact could be related in a way known only to Dr.Evil at the ballot-printing office, permitting him to know trivially how everybody voted.

This attack devastates numerous ideas. Danny Sleator proposed the cheapo semi-secure plan intended to be simpler, more practical, and more like current procedures, than ours (at the cost of only being semi-secure). However, Sleator still needs to debundle, considerably decreasing the attractiveness of his cheapo plan, if he wants to avoid this vote-selling-to-Dr-Evil attack.