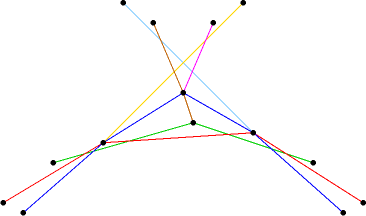
A set of 14 points with 14 halving lines, split into 7 convex chains
A halving line of an n-point set in the plane (n even), shall mean a line
through 2 of the points, with exactly
This section by Jeff Erickson with a few updates by Warren D. Smith 2011 to compute constants explicitly.
The crossing number of a graph is the minimum possible number of intersecting pairs of edges in any planar drawing.
Crossing Lemma (Ajtai, Chvátal, Newborn, and Szemerédi; also indepedently by F.T.Leighton): Any graph with n vertices and e > 4n edges has crossing number> e3/(64n2).
Proof:
Consider a planar embedding of a graph with n vertices, e edges, and
c pairs of crossing edges.
Euler's formula implies
that c > e-3n. (In fact c≥e-3n+6.)
Take a random subset of the vertices, each vertex
with probability p. The expected number of vertices, edges, and crossings in the
induced subgraph are at least pn, p2e, and
p4c, respectively. Thus, p4c >
p2e - 3pn, which implies c >
e/p2 - 3n/p3. Taking p =
4n/e gives us
According to János Pach, this ultra-simple probabilistic proof has been independently rediscovered several times, by Lovász, Matousek, Füredi, Alon, Seidel, and many others, but was not published since it is essentially equivalent to the original counting argument of Ajtai et al. The proof was first published by L.Székely. Using a more complicated probabilistic argument, J.Pach and G.Tóth (Proc. Graph Drawing '96, Springer LNCS 1190, 1997, pp. 345-354) recently improved the constant from 1/64 to 4/135.
Theorem (Dey): Any set of n points in the plane has at most 25/3n4/3 halving lines.
Proof (Dey): Let S be a set of n points in the plane. Let H be the set of line segments with endpoints p,q in S, such that the line through pq is a halving line.
The segments in H can be decomposed into ≤n/2 convex chains as follows. Start with a vertical line through one of the n/2 leftmost points p in S, and rotate this line clockwise around p until it contains a segment pq in H. Initially, there are less than n/2 points above the line; this number goes down whenever the line hits a point to the left of p, and goes up whenever it hits a point to the right of p. It follows that q must lie to the right of p. Continue rotating the line clockwise around q until it hits another segment in H (which will lie to the right of q), and so on, until the line is vertical again. The sequence of segments hit by the rotating line forms a convex chain, and every segment in H is in exactly one convex chain. (These convex chains are dual to the concave chains studied by Agarwal, Aronov, and Sharir.)

The number of intersections between any two convex chains is no more than the number of upper common tangents between the same two chains. Any line between two points in S is an upper common tangent of at most one pair of chains. Thus, there are <n2/2 intersections between the segments in H. By the Crossing Lemma, any graph with n vertices and crossing number c<n2/2 has e<25/3n4/3 edges, so S has at most 25/3n4/3 halving lines, QED.
More generally, Dey's argument can also be made to show an upper bound of 4k1/3n on the number of "k-sets," i.e. lines through two of our n points with exactly k-1 points on one side and n-1-k on the other.
Tamal K. Dey: Improved bounds for planar k-sets and related problems, Discrete & Computational Geometry 19,3 (1998) 373-382.
A "δ-dense" n-point set in the plane has the ratio of its furthest divided by its closest interpoint distance, upper bounded by δ√n.
H. Edelsbrunner, P. Valtr, and E. Welzl: Cutting dense point sets in half, Discrete & Comput. Geom. 17,3 (1997) 243-255
showed that any upper bound O(n1+c) for the number of halving lines could be converted into a stronger upper bound of O(δ2+c n kc/2) for the number of k-sets in a δ-dense n-point set. Hence from Dey's bound we see that
For a δ-dense n-point set in the plane, the number of halving lines is O(δ7/3n7/6).
Also, Nivasch notes that an upper bound O(n1+c) on the number of halving lines implies an upper bound O(n kc) on the number of k-sets (for this, no assumption about denseness is needed), shown by
P.K. Agarwal, B. Aronov, T.M. Chan, M. Sharir: On levels in arrangements of lines, segments, planes, and triangles, Discrete Comput. Geom. 19,3 (1998) 315-331.
Given n points with h(n) halving lines,
place three very stretched copies of that set at the vertices of a very very large
equilateral triangle (each stretched in the direction from the triangle center).
This shows
for an infinite set of even n>0. A different recurrence (which arises by considering replacing each point in the a-point set by a tiny stretched-in-a-suitable-direction b-point set) is h(ab)≥bh(a)+ah(b) from which we deduce starting from h(4)=3 that h(16)≥24, h(256)≥768, h(65536)≥393216, ..., and
for another infinite set of even n>0.
Gabriel Nivasch: An improved simple construction of many halving edges, pp.299-305 in Surveys on Discrete and Computational Geometry: Twenty Years Later (J.E. Goodman et al. editors), Contemporary Mathematics #453, AMS 2008
constructed (for an infinite set of n>0 and some positive constant c) a set of n points in the plane with
halving lines.
Edelsbrunner, Valtr, Welzl constructed 1.5-dense n-point sets with ≥(n/12)log3n-n halving lines for each even n≥2.
| n (# points) | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| max # halving lines | 1 | 3 | 6 | 9 | 13 | 18 | 22 | 27 | 33 | 38 | 44 | 51 | 57 | ? | ? |
(See A076523.) Erdös, Strauss, Lovasz, and Simonovits were the ones who originally invented this whole problem, and in 1973 they conjectured that the number of halving lines for an n point set in the plane is always upper bounded by n1+o(1), i.e. by a constant times n1.001. As of the year 2016, this conjecture remains open.