Fast Implementation of Shortest Splitline Algorithm for Political Districting

Warren D. Smith June 2011

We'll first review what the shortest splitline algorithm is, then explain how to use fancy algorithms techniques from computational geometry, to program it so it is guaranteed to run quickly (even on worst-case input) and with high accuracy (in fact exact if we had exact real arithmetic and knew the exact country-shape and people locations).

This page is intended for perfectionists. Even fairly crude algorithmic approaches suffice to deliver acceptable accuracy in acceptable time on realistic input, so the methods discussed here are not really necessary.

The shortest splitline algorithm (SSA)

Was invented by Warren D. Smith in the early 2000s. It is a very simple mechanical procedure that inputs the shape of a country and the locations of its inhabitants, and a positive number N, and outputs a unique subdivision of that country into N equipopulous districts.

Formal recursive formulation of shortest splitline districting algorithm:

ShortestSplitLine( State, N ){
  If N=1 then output entire state as the district;
  A = floor(N/2);
  B = ceiling(N/2);
  find shortest splitline resulting in A:B population ratio
        (breaking ties, if any, as described in notes);
  Use it to split the state into the two HemiStates SA and SB;
  ShortestSplitLine( SB, B );
  ShortestSplitLine( SA, A );
}

Notes:

1. Since the Earth is round, when we say "line" we more precisely mean "great circle." If there is an exact length-tie for "shortest" then break that tie by using the line closest to North-South orientation, and if it's still a tie, then use the Westernmost of the tied dividing lines.
2. If the state is convex, then a line will always split it into exactly two pieces (each itself convex). However, for nonconvex states, a line could split it into more than two connected pieces e.g. by "cutting off several bumps." (We expect that will occur rarely, but it is certainly mathematically possible.) In either case the splitline's "length" means the distance between the two furthest-apart points of the line that both lie within the region being split.
3. If anybody's residence is split in two by one of the splitlines (which would happen, albeit very rarely) then they are automatically declared to lie in the most-western (or if line is EW, then northern) of the two districts. (An alternative idea would be to permit such voters to choose which district they want to be in.)

Example: The picture shows Louisiana districted using the shortest splitline algorithm using year-2000 census data.

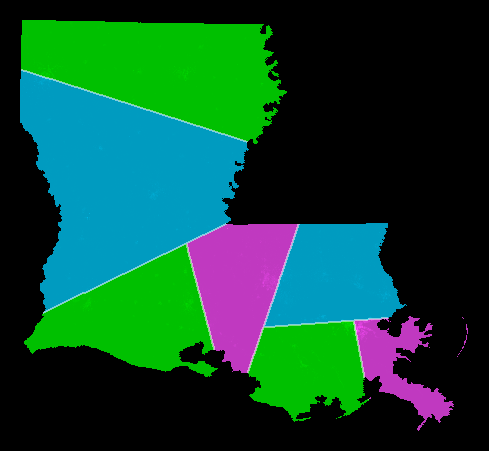
Want N=7 districts.
Split at top level:   7 = 4+3.  This is the NNE-directed splitline.
Split at 2nd level:   7 = (2+2) + (1+2).
Split at 3rd level:   7 = ((1+1) + (1+1)) + ((1) + (1+1)).
result: 7 districts, all exactly equipopulous.

How to make a computer run the SSA very quickly

Theorem (single split-stage of SSA): Given as input:

• The V vertices of the border of the country (assumed to be a simple polygon or collection of simple polygons, can have polygonal holes, use anticlockwise order for outer boundaries and clockwise for inner boundaries). Let V=V_R+V_C where V_R is the number of "reflex" vertices (i.e. bent "the wrong way") and V_C is the number of "convex" vertices (bending toward the interior of the country) of the country-border.
• P people (specified as XY coordinates on the plane); note the people and polygon vertices can also be specified on the sphere using XYZ coordinates or latitude-longitude, and our methods will still work provided all these V+P points lie within the interior of some hemisphere.

A randomized algorithm exists (on a pointer machine with real arithmetic) to find the (exact) "shortest splitline" which splits the population in any specified ratio, in

steps, while consuming O(P+V) memory cells. Here α(x) is an inverse Ackermann function (extremely slowly-growing) while h(P) is the largest possible number of halving lines for a P-point set in the plane. Tamal Dey proved that h(P)≤2^5/3P^4/3, which was improved to by Khovanova & Yang 2012 to h(P)≤[(40/3)(P-1)P³]^1/3 (which reduces the constant factor to 74.7% of Dey's value). A conjecture of Erdös et al says h(P)=P^1+o(1). In the other direction, point sets constructed by Geza Toth show h(P)≥Pexp((lnP)^1/2C) for some constant C>0. [G.Toth: Point sets with many k-sets, Discrete & Computational Geometry 26,2 (2001) 187-194.] Thus given Erdös's conjecture our runtime bound is

steps.

Corollary (full SSA): Given also an integer N with 2≤N≤P, we can run the whole shortest splitline algorithm to subdivide the country into N equipopulous (to within 1 person) districts, in

steps while consuming O(P+V+N) memory cells. Given Erdös's conjecture this runtime bound is

Conjectural Further Speedup: If the country is specified using only a single simple polygon (now no polygonal "holes" nor multiple connected components are allowed; the word "simple" means "not self-crossing") then the "logV" in all the runtime bounds above, can be omitted (i.e. replaced by "1"). If we do allow holes and multiple components then still it ought to be possible to attain

Optimality: These algorithm runtimes and space-usages obviously are optimal to within logarithmic and inverse-Ackermanic factors and a factor of h(P)/P. All of these are slow growing. If this full scheme is programmed it should be extremely fast and accurate, perhaps running in only a few minutes for an entire country using IEEE double precision real arithmetic to find the exact splitline to 9 decimal places, i.e. centimeter accuracy.

Proof (how the algorithm works): We simply combine a lot of known algorithmic results from computational geometry.

1. If we are on the sphere (round earth), then we can perform a gnomonic (central) projection to map everything onto a flat plane in such a way that geodesic segments on the sphere correspond to line segments on the plane. As the central direction of the projection we can use the direction from the Earth-center to the center of the smallest sphere enclosing all the V+P points. This smallest enclosing sphere may be found in O(V+P) steps (Megiddo 1983; or it is simpler to use the approach of Welzl 1991 based on adding the points one at a time in random order). Then the projection can be done in O(1) steps per point, i.e. also in O(V+P) steps.
2. Find the convex hull of the V border-points of the country (and the P people, except since the people are assumed to lie inside the country they can be ignored for this purpose). This takes O(VlogV) steps. We now have a subdivision of that convex hull polygon into polygonal regions, some of which are inside the country and some of which are not. Also subdivide all of these regions further by triangulating them by diagonals in O(VlogV) steps as in Fournier & Montuno 1984.
3. Apply the preprocessing of Guibas, Hershberger, Leven, Sharir, Tarjan 1987 to all those triangulated polygons. This paper in O(V) time builds a data structure in O(V) memory cells allowing arbitrary future point+direction queries to be answered in O(logV) steps per query, where each answer says which polygonal region the query-point is located in, and which border line-segment it sees if it looks in the given direction.
4. Use the algorithm of Har-Peled 2000 (viewed using "point-line duality"; see also Chan 1999) to "visit" each pair AB of people forming a (desired population ratio) splitline for the P people. This algorithm runs in O(α(P)h(P)) steps. For each such pair AB, find the two points where the line through AB hits the convex hull (this may be done in O(logV) time per query using a procedure akin to "binary search") then use the GHLST data structure to "look inward along AB" from those two points to find the two furthest-apart points on AB which lie within the country.
5. To be more careful and exact: "the" splitline corresponding to a person-pair AB is actually a family of splitlines (since the lines do not actually go exactly through a person, and we allow 1 extra person on one side of the line than the other). Each family consists of all the lines lying between two particular lines, and our description last step was really only about finding the bounding-lines for each such family. We can use Har-Peled's methods to visit each such family. There actually is not just one point on the country-border on each end of this line, but rather the whole line-family intersects the country border (at each end) at two sets S_A and S_B of line segments (and partial line segments). We then need to find the shortest line within that whole family. It is best to include the reflex vertices of the country-border polygon(s) as artificial extra "people" (used for the purpose of finding splitline family-boundaries AB, where A and/or B are allowed now to be artificial people, but not used for the purpose of reckoning population-counts on each side of the line; Har-Peled's algorithm can be made to handle this refinement). This is why the terms in the runtime bounds arising from Har-Peled's algorithm involve not P but rather P+V_R. The task of finding the shortest splitting line-segment in the family may be accomplished by building the Voronoi diagram of all the L line segments in S_A (using construction algorithms by Yap 1987, or Boissonnat et al 1992, preprocessing them for fast point-location using Kirkpatrick 1983 or Sarnak-Tarjan 1986) in O(LlogL) time, then querying using all the points in S_B [each query takes O(logL) steps; also I think all this can be done using GHLST's data structure] to find the closest S_A-point to each (and vice versa with the roles of A & B interchanged) and computing exact distances from points to line-segments (and using the true-spherical distance formula if problem originally posed on round earth). Note that due to including all the reflex boundary-vertices as "artificial people" each such family only intersects the boundary polygons on convex chains and of course we discard out all but the outermost two chains for this purpose.

Notes on the conjectural further speedup: A V-vertex simple polygon can be triangulated in O(V), not VlogV time using an extremely complicated algorithm by Chazelle 1991 (see also Amato, Goodrich, Ramos 2000). The GHLST data structure then can be built in O(V), not VlogV, time for a simple polygon. The convex hull of a single simple polygon can be found in O(V), not VlogV time using a method related to the "Graham scan."

The Voronoi diagram of the vertices of a convex V-vertex polygon can be built in O(V), not VlogV time using a method of Aggarwal & Shor 1987. (This is relevant to the final step of our algorithm involving convex subchains S_A and S_B of the polygonal boundary.) This suggests that the distance between two convex polygonal chains, with V vertices in all, both inward-bending, should be computable in O(V) not VlogV time. (That was already known using 2D convex-programming methods if they both are outward-bending and with disjoint convex hulls.) I suspect by some "moving fingers" methods the need for the GHLST data structure can be eliminated and so can the need for the binary-search-like procedure on the convex hull, but we nevertheless could obtain O(1) query-time in an "amortized" sense.

Notes for practical programmers (as opposed to algorithm-theoreticians who want theoretical guarantees): In practice I would recommend a number of shortcuts to make programming simpler without costing much:

• I would not use the whole set of people, I'd use some random subset with only, say, (PNlogP)^1/2 people, which ought to provide good enough accuracy almost certainly comparable or smaller than errors the census has anyway. (And if you want more pseudo-accuracy, later refinement could be done using the full population.)
• I'd skip the final step (or rather, use some simplified form of it). That is, the whole point that really, any two people-subsets separable by a splitline are in general separable by a family of splitlines, is for real populations in real countries, not going to matter much since it only allows improving splitline lengths by tiny amounts. since the families will be very "thin" and only intersect the country boundaries on very short subsegments. If so, these can be dealt with by brute force rather than the fancy Voronoi-diagram building and point-location (asymptotically efficient) method.
• The whole (very complicated) GHLST data structure could be omitted if your country borders are not insanely wiggly, by keeping track of a number of "fingers" on the borders which all move around slightly as Har-Peled's lines move around slightly (he visits them in a nice order which doesn't do a lot of "motion").
• I'd not even attempt to program the "further speedup."

References

A. Aggarwal, L. Guibas, J. Saxe, P. Shor: A Linear time algorithm for computing the Voronoi diagram of a convex polygon, Discrete & Computational Geometry 4 (1989) 591-604. See also L.Paul Chew: Building Voronoi Diagrams for Convex Polygons in Linear Expected Time, (1990) Dartmouth Dept. of Math & Computer Science PCS-TR90-147.

Nancy M. Amato, Michael T. Goodrich, Edgar A. Ramos: Linear-Time Triangulation of a Simple Polygon Made Easier Via Randomization, In Proc. 16th Annu. ACM Sympos. Comput. Geom SoCG (2000) 12pp

Jean-Daniel Boissonnat, Olivier Devillers, Rene Schott, Monique Teillaud, Mariette Yvinec: Applications of Random Sampling to on-line algorithms in computational geometry, Discrete & Computational Geometry 8,1 (1992) 51-71.

Timothy M. Chan: Remarks on k-level algorithms in the plane (1999).

Bernard Chazelle: Triangulating a simple polygon in linear time, Discrete & Computational Geometry 6 (1991) 485-524.

Steven J. Fortune: A sweepline algorithm for Voronoi Diagrams, Algorithmica 2,2 (1987) 153-174.

A.Fournier & D.Y.Montuno: Triangulating simple polygons and similar problems, ACM Trans.Graphics 3,2 (1984) 153-174. [O(NlogN) algorithm and O(N) if begin from a "trapezoidation."]

Leonidas Guibas, John Hershberger, Daniel Leven, Micha Sharir, Robert E. Tarjan: Linear-time algorithms for visibility and shortest path problems inside triangulated simple polygons, Algorithmica 2,1-4 (1987) 209-233.

Sariel Har-Peled: Taking a walk in a planar arrangement, SIAM J. Comput., 30,4 (2000) 1341-1367.

D.G.Kirkpatrick: Optimal Search in Planar Subdivisions, SIAM J.Computing 12,1 (1983) 28-35.

Nimrod Megiddo: Linear-Time Algorithms for Linear Programming in R³ and Related Problems, SIAM Journal on Computing 12,4 (1983) 759-776.

Neil Sarnak & R.E. Tarjan: Planar Point Location Using Persistent Search Trees, Communications of the ACM 29,7 (1986) 669-679.

"Soft-surfer" guide to O(NlogN)-time algorithms to compute convex hull of N points in plane.

Emo Welzl: Smallest Enclosing Disks (Balls and Ellipsoids), pp.359-370 in H. Maurer (Ed.), New Results and New Trends in Computer Science, Springer Lecture Notes in Computer Science #555, (1991). See also Bernd Gärtner: Fast and Robust Smallest Enclosing Balls, Proc. 7th Annual European Symposium on Algorithms (ESA), Springer Lecture Notes in Computer Science #1643, pp.325-338.

Chee K. Yap: An O(n log n) Algorithm for the Voronoi Diagram of a Set of Simple Curve Segments, Discrete & Comput. Geometry 2,4 (1987) 365-393.

Return to main page