
(2 copies laid
end-to-end
to fill square
not triangle)

By Warren D. Smith. PRELIMINARY 2nd draft July 2011. warren.wds AT gmail.com
RETRACTION. Sorry, this paper-in-progress has been largely wrecked by my too-late realization that the expectation-side of my fundamental two-sided distance inequalities, are just wrong. The corrected inequalities will have the form
for positive constants A, B. Note the "log." So most of the stuff here can be rescued once weakened by a log factor, but I have to work on that.
Abstract. For several important geometrical optimization problems in the plane involving minimizing sums of squared distances – e.g. the "traveling salesman problem" with sum of squared hop-lengths as costs, and most prominently the "optimum political districting" problem – we devise extremely efficient and simple randomized "approximation algorithms." These algorithms construct a solution that is optimal to within a factor of K, where K is a random variable (depending on random numbers generated within the algorithm) with Expectation(K)<6.38. The methods employ randomly rotated, translated, and scaled suitable "space filling curves." You simply sort the input sites along such a space-filling curve and solve the resulting one-dimensional problem optimally; then you argue this magically yields expected-6.38-approximation of the optimum solution of the original 2D problem.
We also offer appealing new results in pure geometry supporting senses in which the plane-filling curve by Sierpinski is the uniquely "best," and a new plane-filling curve by Peano and Smith is the uniquely "second best," among all plane-filling curves. Let a "halvable" ("trisectable") object in d-space be one that can be cut into two 2-1/d-scaled (three 3-1/d-scaled) copies of itself, perhaps including mirror-congruences. We prove that the 45-45-90 right triangle and parallelograms with sidelength ratio √2 are the only halvable, and parallelograms with sidelength ratio √3 the only trisectable, convex 2-dimensional objects. Nonconvex examples also exist, but they all have "fractal" boundaries with infinite arclength. Halvable and trisectable parallelipipeds exist for each d≥1, but for d=3 we prove that no halvable nor trisectable tetrahedra exist.
Definition: A "good space-filling curve" is one that meets the following criteria:
Peano in 1890 constructed the first good (also very good) spacefilling curve, which has Δ=κ=1 and s=9. Let us now enquire about the limitations of these criteria.
THEOREM of the necessity of curve-self-intersection: A curve obeying criteria 1 and 2 cannot yield a total ordering. Indeed, the exceptional set E must contain an infinite and dense set of points, such that the curve visits each of them at least d+1 times.
Proof: This follows immediately once you know about Brouwer/Lebesgue covering dimension aka topological dimension. (more details???) QED.Peano's original (d=2) curve meets this bound – for his curve, E consists entirely of 3-time-visit points, and points in E all have x- and y-coordinates which both are rational with denominator that is a power of 3 (hence E plainly is countable). Hilbert in 1891 gave another good spacefilling curve (having s=4 and Δ=κ=1) in which E consists entirely of 4-time-visit points, and all points in his E have x- and y-coordinates both rational with denominator that is a power of 2.
Almost-total ordering as in criterion 3 is good enough to define an inverse function for the curve, i.e. mapping (x,y) to t in a manner which is single-valued on all but a countable subset E of the xy plane, and boundedly-multivalued even on E. This kind of inverse is very useful because of the
SORTABILITY THEOREM: Any measure-zero subset of d-space, if randomly translated (with optionally also a random rotation) then with probability=1 will enjoy a unique 1-dimensional order along any good space-filling curve.
Proof: This is because if we rotate and translate your point set randomly, then it will with probability=1 not intersect E, since E is countable and the measure of a union of countably many measure-zero sets still has measure=0. Hence our inverse will provide a unique ordering. QED.
Definition: A good plane-filling curve is algorithmic if there is algorithm which, given t and an ε>0, will compute the xy coordinates of the curve point with parameter t, accurate to within ε; and if instead given the xy coordinates, will compute t accurate to ±ε if (x,y)∉E, and if (x,y)∈E will compute at least one of the values of t corresponding to it, accurate to ±ε.
Corollary: As special cases of the sortability theorem any countable set is sortable and any finite set is algorithmically sortable if we use any algorithmic good space-filling curve. All the space-filling curves we are going to use in this paper are algorithmic and the algorithms run in O(|logε|) operations.
NOWHERE-DIFFERENTIABILITY THEOREM: A curve obeying criteria 1, 2, and 4 necessarily is nowhere-differentiable.
(The proof is trivial.) Henri Lebesque in 1904 (see Sagan 1993) found a curve filling the unit square which was, in contrast, differentiable at almost every t – the domain of nondifferentiability is a measure-0 "Cantor set." Lebesque's curve will not be of interest to us because it disobeys our uniformity criterion 4.
INTEGRALITY CONJECTURE: For a good space-filling curve in any dimension d≥2, the scaling factor s>1 must be an integer.
If s is not an integer, then very amazing things would happen – too amazing, I suspect, to actually occur. Suppose for simplicity that Δ=1 so the inter-integer subsegments of the real t line yield a tiling of the plane. However, using step-size sK, for any fixed integer K, also yields a tiling. By choice of K we can make sK arbitrarily close to (but not) an integer. So then we have a very peculiar thing: an area=1 tile T which tiles the plane by itself, but also tiles it in a fixed ratio with a second tile U (the T:U ratio depends nontrivially upon U and can become arbitrarily large), where the second tile can be selected in an infinity of ways, and its area can be specified to be any member of a set everywhere dense in the positive reals, and its diameter can be demanded to be arbitrarily small... and for any subset of all these infinity of possible (all non-similar) tiles, we can tile the plane using all members of that subset in fixed ratios.
INTEGRALITY THEOREM: For a very good space-filling curve in any dimension d≥2, the scaling factor s>1 must be an integer.
PROOF??? this is going to be obvious later.
In the next section we shall construct various curves showing
ACHIEVABILITY THEOREM: If s≥2 is an integer it is achievable as the scale factor of an algorithmic very good plane-filling curve if either s is odd, s=2, s is a square, or s is any power of an achievable s (for example any power of 2).
Thus achievable scale factors include 2, 3, 4, 5, 7, 8, 9, 11, and 13, with the first three unclear cases being s=6, 10, 12. Indeed, s=4, 5, and 7 each are achieveable via at least two, and s=9 via at least three, quite-different good curves.
Incidentally none of the above theorems/conjectures are stated in apparently the only extant book (Sagan 1994) on this topic. They all seem new – except that some version of the necessity of curve-self-intersection theorem must already have been known, since various authors keep noting this without any hint of a proof.
Let x and y be real numbers in the 1×1 square 0≤x<1 and 0≤y<1. In 1891 David Hilbert recursively defined a map H(x,y) from (all but a countable subset of) this square to the real interval [0,1). The inverse map exists and is continuous and can be regarded as a "space-filling curve," parameterized by t, filling the 1×1 square. It has s=4, Δ=κ=1. A closely related curve was defined by Eliakim H.Moore in 1900 (it's actually just 4 Hilbert curves laid end to end). Some less-related curves were found by Walter Wunderlich in 1973 (cf. Sagan §3.7); They each have s=9, Δ=κ=1. It is easy to generalize the Hilbert/Wunderlich idea to construct good plane-filling curves with any scaling-factor s>1 that is any square, s=4, 9, 16, 25, 36,... Waclaw F.Sierpinski in 1912 defined a different curve obeying these same claims, via a different such map S(x,y); this curve was rediscovered and/or clarified by G.Polya 1913 and K.Knopp 1917. It has s=2, Δ=κ=1. All the curves we've mentioned so far are continuous everywhere but differentiable nowhere.
The scale-invariance, aka self-similarity, property of these curves can be used to regard them as actually filling the entire xy plane, not merely the unit square, and now parameterized by t on the the full real line.
R.William Gosper in ≈1973 defined yet another interesting space-filling curve with s=7, although his is no longer based on the unit square, but rather on a different plane-tessellator, somewhat resembling a regular hexagon, called the Gosper snowflake or Gosper Island. (See Gardner 1976. Its algorithmicity was shown by Ed Schouten, although Gosper presumably also knew it.) H.Fukuda, G.Nakamura and collaborators during 2000-2007 defined a set of conditions for a curve to be a "Gosper-like space-filler" and proved an infinite number of different such curves exist, of which Gosper's is the simplest. Theirs have scaling factors s=7,13,19,31,37,43,... all of which are 1 mod 6 and representable as a²+ab+b² for integers a,b≥0 (but note 25=0²+0·5+5² is missing). There also is a nice space-filling curve with scaling factor s=5 constructed by Robert Ferreol and Jacques Mandonnet in 2002, although apparently known earlier. Their idea is essentially the same as Gosper's but based on the square rather than equilateral-triangle grid. It should be generalizable to get curves with other scaling factors s=a²+b² with s≡1(mod 4). But Gosper's and Ferreol-Mandonnet's curves are merely "good" and do not qualify as "very good" since the Gosper Island has infinite perimeter.
I have a new construction, closely related to Peano's original 1890 construction, which yields a good planefilling curve with any odd integer scaling factor s≥3. The Hilbert, Wunderlich, Sierpinski, and Peano-Smith constructions all can be concisely summarized via "recursive definition diagrams," see figure 1.

The Gosper and Ferreol-Mandonnet constructions could also be described via such diagrams but it would not be easy to draw them because instead of the simple shapes (isoceles right triangles, squares, and rectangles) needed for the Sierpinski, Hilbert, and Peano-Smith diagrams, now certain new shapes, mildly resembling regular hexagons and squares but having fractal boundaries, would be required. The important thing is that
It is easy to see from our definition of "good space-filling curve" that every such curve with integer s has at least one definition expressible via such a diagram, with the shape being one of the fundamental tiles guaranteed in the definition's criterion 5, in which that shape is tiled by s copies of an s-1/d-scaled version of that same tile.
| Hilbert |

|
| Sierpinski (2 copies laid end-to-end to fill square not triangle) |

|
| Gosper |
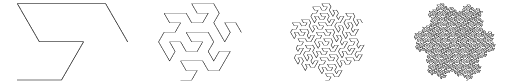
|
To illustrate how to convert recursive definition diagrams into algorithms let me discuss my own variation of the first-ever discovery of space-filling curves by Giuseppe Peano in 1890. Peano's construction can be regarded as based on the fact that a 3×3 square can be cut into three 3×1 rectangles (and then into nine 1×1 squares). Do essentially the same thing, but instead using the fact that a 1×√s rectangle can be cut into s different (√s×1)/s rectangles. Using this, recursively, we can devise a space-filling curve symmetric under scaling the plane by √s, for any odd s≥3. For the simplest case s=3 we define the Peano-Smith map t=P(x,y) mapping the set {0≤x≤1, 0≤y≤√3} to the real interval 0≤z≤√3 recursively via
| 0/√3 + P(y√3,x√3) | if 0≤y<1/√3 | ||
| P(x,y) = | 1/√3 + P(y√3-1,(1-x)√3) | if 1/√3≤y<2/√3 | |
| 2/√3 + P(y√3-2,x√3) | if 2/√3≤y≤√3 |
and P(0,0)=0 and P(1,√3)=√3.
On the left below, we exhibit a P(x,y) algorithm based on the above definition (now valid for general odd s≥3). On the right, we give another algorithm – a simplification of code by Bartholdi – for Sierpinski's S(x,y) [doubled curve, filling unit-square]; this illustrates the possibility of organizing the computation by converting the recursion to an iteration going "bottom up" rather than the "top down" approach we used for P(x,y). In that algorithm ε denotes the least positive real number such that the computer believes 1+ε>1.
real P(real x, real y, const integer s){
real δ,t;
integer c;
if(x<0 or x>1 or y<0 or y>√s) return(ERROR);
if(s<3 or s mod 2=0) return(ERROR);
t ← 0; δ=1.0/√s;
loop{
c ← floor(y√s);
t ← t + c×δ;
if(c mod 2≠0){ x ← 1-x; }
(x,y) ← (y√s-c, x√s);
δ ← δ/s;
}while(1+δ>1); //stop when computer thinks 1+δ=1
return(t); // will range between 0 and √s
}
|
real S(real x, real y){
real t,u;
const real δ = ε²/8;
if(x<0 or x>1 or y<0 or y>1) return(ERROR);
t ← 0; u ← 1;
if(x>y){ t ← t+δ; x ← 1-x; y ← 1-y; }
while(u>ε){
t ← 2×t;
if(x+y>1){ t ← t+δ; (x,y) ← (1-y, x); }
x ← 2×x; y ← 2×y; t ← 2×t;
if(y>1){ t ← t+δ; (x,y) ← (y-1,1-x); }
u ← 0.5×u;
}
return(t); // will range between 0 and 1
}
|
Every space-filling curve necessarily has infinite length. However,
we shall regard the |difference| in t-values of two generic points in the plane
as the "one-dimensional distance"
between them, as opposed to the usual two-dimensional distance
It is also possible to fill the d-dimensional hypercube with a curve for any fixed dimension d, e.g. using the d-dimensional Hilbert curve, albeit we'll mainly stick to d=2 in this paper. A famous theorem of Hahn & Mazurkiewicz (see Sagan 1994) indeed shows that space-filling curves exist not only in any dimension but indeed in any abstract "locally connected metrizable space."
Let T be a "fundamental tile" for our curve, i.e. corresponding to the subinterval 0<t<Δ of the real t line. Let s>1 be the curve's scale factor. For the Hilbert (s=4) and Sierpinski (s=2) curves we can simply let T be the unit square; for the Peano-Smith curve use a 1×√s rectangle.
Definition of randomized curve: We imagine translating the curve bodily by a random vector in T, rotating it by a random-uniform angle θ with 0≤θ<2π, and finally scaling all coordinates by a multiplicative factor of sQ/2 where Q is random-uniform with 0≤Q<1. (All randomness assumed independent.)
(Alternate view: We can also keep the curve fixed and rotate/translate/scale everything else. The effect will be the same.)
The inequality
proves continuity of Hilbert's curve. Note, I have really only proven this for the slightly weaker constant 6.001, but have no doubt the truth is exactly 6. One's computer can prove upper bounds arbitrarily near to best possible as follows. We first prove a trivial weaker constant, here 20, manually; then the computer exhaustively examines all possible point-pairs within a tile with some finite accuracy δ>0. This yields stronger bounds, approaching the strongest possible bound in the limit δ→0+. The constant 6 would be tight since it arises in a limit where
Since it is impossible to get continuity for the inverse (i.e. dimension-decreasing) map, there can be no inequality in the other direction, i.e. two points in 2D can be brought arbitrarily close together while keeping their 1D distance above a positive constant.
However, suppose before computing the t-values corresponding to a set of 2D points, we first randomly pre-rotate, pre-translate, and/or pre-scale that point set, as described last section, using a random translation by a random-uniform member of sKT for some integer K chosen so that sKT is large enough to contain our point set, We then effectively have a family of space-filling curves parameterized by the rotation angle θ, the translation vector (Δx, Δy), and Q (the logs of the scaling factor), from which we are randomly selecting one such curve.
In that case, we do get a reverse-direction inequality in expectation, namely
THIS IS WRONG, THE COMPUTER AND I WERE CONFUSED BY LOG-INFINITY. But it should be possible to re-do to prove a logarithmically-weaker bound of this kind.
The constant 0.6371 in this bound is an underestimate of the strongest possible constant whose true value is somewhere in [0.6371, 0.6372]. I computed this using numerical integration. Note that numerical integration can be made to yield rigorous arbitrarily tight error bounds by using the continuity bounds for the space-filling curves.
It is important to realize why 0.6371 is neither infinity nor zero. Here is the precise way it arises:
where the tj is computed from (xj, yj) using Hilbert's t=H(x,y), and where the endpoints (x1, y1) and (x2, y2) of the line segment are got by
Obviously, then, we are never dividing by 0. In fact, we are dividing by the square of a 2D-distance which always is bounded between s-1 and 1. Further, the 1D-distance is always bounded between two positive constants. So we are computing the expectation of a bounded and always-positive random variable, hence necessarily get a bounded and positive result.
For the Peano-Smith curve [as defined by our P(x,y) algorithm above with s=3]
Regarding 4.6183, a number slightly below 4.6182460878 arises from
The strongest possible value of 0.6377 is somewhere in the interval [0.6377, 0.6379].
In arbitrary dimension d: The Peano-Smith curve can be defined, not just in d=2 dimensions, but in fact for any d≥2. The recursive definition diagram for the Peano-Smith curve involves cutting a
hyperrectangle R into three by trisecting its longest sides with two parallel hyperplanes. The resulting three hyperrectangles R1, R2, R3 each have exactly one-third the d-volume and each have the same shape as R. The "arrows" inside each rectangle join one of its vertices to an antipodal vertex. Let us agree to choose the units of time so that 1 time unit corresponds to 1 unit of d-dimensional spatial volume.
We compute
We wish to find positive constants Ad and Bd such that
We obtain x1 and x2 by starting with a standard unit-length line segment then performing a random rotation, transatlion, and scaling as in §3. We may assume wlog that x1∈R. However x2 might not be in R. If not, it will necessarily lie in one of the 2d neighboring boxes. It unfortunately is possible for one of those boxes to be arbitrarily huge, lie in different Rj since otherwise we could just recurse downward and regard the comon Rj as R. Hence DistdD[x1, x2]2≤diam(R)2 and Expect(DistdD[x1, x2]-1) can actually be computed in closed form in low-enough dimensions, e.g. when d=2 we have
mean 1/dist in a 1xB rectangle where one point is in top half, other in bottom half, is H := (B) -> 4*B^(-2)* int(int(int(int( 1/sqrt((x-u)^2 + (y-v)^2), u=0..1), x=0..1), v=0..B/2), y=B/2..B); ≤diam(R)2 Dist1D[t1, t2]≥???
For Sierpinski's (doubled) curve [as defined by Bartholdi's S(x,y) algorithm above]
The constant 4 again really means that all I really have proven is 4.001. The truth undoubtably is exactly 4 though, and this would be tight since it arises if
via a suitable combined limiting process. Sierpinski's curve is optimal in the sense that 4 is least possible for any closed curve filling the unit square, as you can see by considering its four corners.
Note also that 0.62725 is only approximate; the true value of this constant is somewhere in [0.62725, 0.62729]. This was found via numerical integration. (It actually ought to be possible to compute the 0.6273, 0.6371 and 0.6378 constants in closed form, but I have not exerted the effort.) For our purpose it is best to minimize the ratio of these two constants. Sierpinski's curve is better than Hilbert's for our purposes, since for it the ratio is <4.001/0.62725<6.38 while Peano-Smith3 would have yielded about 7.24 and Hilbert about 9.42. We shall use this Sierpinski curve from now on.
Interesting Open problem: What is the best possible space-filling curve?
It turns out that Gotsman & Lindenbaum 1996 studied almost exactly the same quality-measuring ratio as ours. Gotsman & Lindenbaum's measure was not rotation, scale, or translation invariant, and forced everything to be based on a fixed unit square (or more generally unit hypercube), hence is of less interest than ours and probably should be abandoned. But it ought to be within a constant factor of our measure in any fixed-dimensional space. Their measure, they showed, was bounded between 2d-1 and (d+3)d/22d in d-space, and these bounds when d=2, which are 3 and 20 respectively, they showed by special 2D analyses could be improved to 3.25 and 6.67 respectively. The analysis underlying their 2D upper bound 6.67 was questioned by Alber & Niedermeier 2000, who rendered the flaw moot by improving the upper bound to 6.5. I now point out that the 2D Hilbert curve if analysed precisely, instead of (as they did) approximately, improves their upper bound to 5.22. The Peano-Smith (s=3) curve (provided it is ok to redefine things based on a 1×√3 rectangle instead of 1×1 square) would improve it further to about 3.75. Finally the Sierpinski curve (doubled to fill the 1×1 square) improves it even further to 3.45, which nearly meets Gotsman & Lindenbaum's claimed lower bound 3.25 (and their lower bound ought to be improvable with more computing). So Sierpinski's curve appears to be within ≈5% of best possible. See §12 & 13 for results and conjectures suggesting Sierpinski is the uniquely best planefilling curve. The Gotsman-Lindenbaum quality measure for Gosper's curve (redefined to be based on a Gosper Island instead of the unit square) is 8.18, worse than any of our three.
Given N point sites in the plane, the TSP is the path which visits each site exactly once and has minimum total cost. In most uses, the "cost" is the "length." However, we can also consider making the the cost be the sum of the N-1 squared edge-lengths. In that case, here is an extremely simple algorithm for producing an approximately optimum TSP:
Note that this algorithm returns the exact same probability distribution of TSP paths regardless of how the original point set was rescaled, rotated, or translated.
TSP Approximation Theorem: The expected cost of the algorithm's TSP path, is at most 6.38 times the minimum possible cost achieved by the optimal path (even for the worst N-site set). Indeed, it is at most 6.38 times the cost of the minimum spanning tree (MST), which has minimum cost among all connected graphs.
Proof: Consider the optimum TSP path (or MST) edge by edge. For any particular edge, 4 times each edge's "1D length" (|difference| between its endpoints' t-values) is at least the squared 2D length. Our algorithm finds the path with shortest 1D length, which cannot be longer. In other words, our algorithm minimizes a rigorous nonprobabilistic upper bound on the TSP cost, instead of minimizing the cost itself. Now by linearity of expectations this upper bound, when applied to the true-optimum TSP path, will yield a result at most 6.38 times too large, in expectation. Hence the path our algorithm finds, which minimizes that upper bound, must do at least as well. QED.
Remarks: This approach was invented in the late 1980s by Bartholdi & Platzman for the purpose of approximating TSP using the usual (sum of unsquared edge lengths) cost measure. However, their method did not randomize over rotations, translations, or scalings. Empirically they found that their approximation ratio was usually much better than our worst-case bound 6.38 (and it could be further improved by "local optimization" postprocessing). E.g. Bartholdi on his web pages claims Paul Goldsman found the Sierpinski curve yielded 1.34 length-approximation factor for a plane TSP of 15112 German cities. Platzman & Bartholdi 1989 found for N sites random-uniform in the unit square that their algorithm returned tours with length LPB(N) where (with probability →1)
The small but nonzero difference (they estimated it was 0.00002) between the liminf and limsup traces to the fact that B&P's version of our algorithm was specific to the 1×1 square, not scale-invariant. Meanwhile it is known that the length LOPT(N) of the truly-shortest TSP is with probability→1 asymptotic to
(the estimate 0.712 is by Percus & Martin 1996 and Johnson et al 1996). Thus, for random-site input, our algorithm will achieve approximation factor≈956/712≈1.34 for TSP length with probability→1 in the limit N→∞. P&B's most impressive result was a proof that their length-approximation ratio was O(logN) even with worst-case locations for the N sites. That is asymptotically tight within a constant multiplicative factor because a point set which causes length-approximation ratio≥(log2N)/6 was constructed by Bertsimas & Grigni 1988 – and B&G speculated that simply N points equispaced along a random line, will also yield order-logN growth. This speculation must be wrong since it contradicts our results. More precisely, it is ok for Bertsimas & Grigni's counterexamples to happen on special lines, but on generic lines such counterexamples either must not happen, or must have constant factors (e.g. multiplying the logN) which depend on the line such that the effect if averaged over all lines is not growth of order logN.
To explain what I mean by that, the function F(n,q) = 1+q-2n could be described, for any fixed q>0, as featuring "growth of order n." However, if we average F(n,q) for any fixed n over all integers q>0, we get Favg(n)=1. This does not feature growth of order n.
We now see that sum of squared edge lengths is the "right" cost measure – P&B were handicapped by concentrating on the "wrong" one, based on unsquared lengths and hence unfriendly with plane-filling curves – and yields factor≤6.38 approximation (in expectation over random pre-rotations, translations and scalings of the point set) no matter how large N is and no matter how evilly the site-locations are chosen. As far as I know this cost measure had not been previously considered. It can also be thought of this way: for each TSP edge draw a circle in the plane with that edge as its diameter; the task is to minimize the sum of the circle-areas. [Also, since energy of a mass=m velocity=v object is mv²/2, the sum-of-squares TSP cost corresponds to the energy cost of traveling each hop in a fixed amount of time, assuming no frictional losses and no energy recovery on slowdown.] More generally in d dimensions appropriate space-filling curves would yield constant factor (expected) approximation for the sum of dth powers of the edge lengths.
Markov's inequality
for any non-negative random variable q then allows us to, e.g., rerun the algorithm R=K/ε times (independent random numbers each time) to gain confidence>1-2-K that the best TSP found during the R runs, is ≤6.38/(1-ε) times optimal cost. To make that more concrete we can assure at most 7× optimal cost (with confidence>99%) by taking the best TSP found in 47 runs, and then doing 47 more runs would boost the confidence to 99.99%. Since finding this kind of TSP is just sorting, the proposed algorithm is extremely efficient – it runs in O(NlogN) steps using standard sorting algorithms once all the N different t-values have been computed – and also updatable efficiently, in O(logN) steps per update, when sites are added or deleted. One could also, e.g. use 1-dimensional dynamic programming to find the shortest TSP in which every step we hop to a site within ±M of the current site in Sierpinski order. The algorithm we have suggested uses M=1, but any small number M could be employed instead to find the best such TSP in O([2M]! N) steps.
Given N point sites in the plane, each pre-labeled with a positive integer vk for k=1,2,3,...,N, the task is to find the least-cost graph (made of inter-site line segments) with valence vk at site k. (Of course, ∑kvk must be even.) Here "cost" is the sum of the suqared edge lengths. Algorithm:
Specified-valence-graph Approximation Theorem: The expected cost of the algorithm's graph is at most 6.38 times the best possible graph's cost.
The proof should now be trivial once it becomes clear to you that the greediness in step 3 finds the exact optimum for the costs based instead on 1-dimensional distance.
A related task is the same but now also demanding that the graph be connected. That may be accomplished by putting in the approximate TSP path from last section, then decreasing all valences by 2 (but only by 1 for the two path-endpoints), then filling in all remaining graph edges using this section's algorithm (but disallowing edges between sites consecutive in Sierpinski order, since they are already taken by the TSP).
Specified-valence-connected-graph Approximation Theorem: The expected cost of this algorithm's graph is at most 6.38 times the best possible graph's cost.
Given N point sites in the plane, the optimum K-means-clustering task is to find (another) set of K point "facilities" such that the sum over all sites of the squared distance from that site to its nearest facility, is minimum possible. Here is an extremely simple algorithm for producing an approximately optimum K-means clustering:
Alternatively we can in O(N2K) steps use 1-dimensional dynamic programming to actually find the best 2D clustering subject to the constraint that each cluster consists of sites consecutive in Sierpinski order. This will be even better.
K-means approximation Theorem: The expected cost of the algorithm's K-means clustering, is at most 6.38 times the minimum possible cost achieved by the optimal K facilities (even for the worst possible N-site set in the plane).
Proof: Again, our algorithm minimizes a rigorous upper bound on the K-means optimum cost, instead of minimizing the cost itself. By linearity of expectations this upper bound, when applied to the true-optimum site-facility squared lengths will yield a result at most 6.38 times too large, in expectation. Hence the clustering our algorithm finds, which minimizes that upper bound, must do at least as well. QED.
Remarks: Arthur & Vassilvitskii 2007 invented a simple randomized algorithm which could guarantee factor≤8[2+lnK] approximation in expectation (in any fixed-dimensional space). The present <6.38 guarantee is superior since it does not depend on K and also yields a smaller constant for every K≥2; but our method only works in 2 dimensions while their works in any space dimension. Kanungo et al achieved factor 9+ε approximation in d dimensions in runtime O(N3ε-d) but this is inferior to our result if d=2 (plus far more complicated). Mettu & Plaxton 2004 argued that a subsample of only O(Klog(N/K)) sites (obtained via a certain nontrivially biased random sampling algorithm) is with high probability all we need to know about to do a good job, which allowed them, in any fixed dimension d, to obtain an O(1)-factor approximation (with high probability of validity) in O(KN) steps provided logN≤K≤N(logN)-2. Due to this proviso, their result is inferior to ours in 2 dimensions (plus their methods are far more complicated), but for most purposes in low dimensions M&P's methods should be excellent. Our clustering from the Sierpinski curve can be fed into a local-optimization algorithm (such as Lloyd's algorithm) to improve it and the approximation in practice will usually be much better than 6.38.
Given P point sites in d-dimensional space and an integer N with 0<N<P, the task is to find N closed balls (in general of differing sizes), with minimum possible summed d-volume, covering all the sites. Algorithm:
Disc-Covering Approximation Theorem: The expected cost of the algorithm's covering is at most 6.38 times the minimum possible cost (even for the worst possible selection of locations for the P sites) when d=2, and in general dimension d≥3 the same is true if 6.38 is replaced by an appropriate dimension-dependent and curve-dependent constant.
Given P point sites in the plane, the optimum N-district map for those P "people" is a set of N "district centerpoints" (0<N<P) such that the sum over all sites of the squared distance from that site to its district centerpoint, is minimum possible, and each district contains exactly P/N people and each person resides in exactly 1 district. Here is an extremely simple algorithm for producing an approximately optimum N-district map:
Political Districting Approximation Theorem: The expected cost of the algorithm's N districts, is at most 6.38 times the minimum possible cost achieved by the optimal districting (even for the worst possible selection of locations for the P people).
Proof: Again, our algorithm minimizes a rigorous upper bound on the optimum cost, instead of minimizing the cost itself. By linearity of expectations this upper bound, when applied to the true-optimum site-facility squared lengths will yield a result at most 6.38 times too large, in expectation. Hence the districting our algorithm finds, which minimizes that upper bound, must do at least as well. QED.
Remarks: The sum-of-squared-distances cost measure was introduced by Weaver & Hess in the 1960s and further examined by Spann-Gullotta-Kane 2007. Until now it had been open whether any polynomial time algorithm (or randomized algorithm) could guarantee any constant factor approximation for either this, or two other, appealing cost measures. Again the districting from the Sierpinski curve can be fed into a local-optimization algorithm to improve it.
Well-shapedness: Using a "very good" plane-filling curve will automatically yield well shaped political districts.
Dithering: The dithering task is this. We are given a grey-scale image. We wish to replace it with a collection of black dots (so that pure black-and-white printing can be used, with no grey levels) that "looks the same." Witten & Neal 1982 suggested a dithering algorithm involving a plane-filling curve. You walk through the image's pixels in the order arising from the curve, keeping track of the greyscale totals for pixels encountered since the last black dot. Every time that total exceeds some fixed threshold, you put a black dot and reset the running total back to zero. (As a slight improvement, we suggest locatng the black dot not at the final pixel, but rather the one midway in the order between the first and last.)
Dithering can pretty much be considered to be the same task as the political districting problem if we change "grey scale"→"population density" and "black dot"→"district representative" or "district center"! Previous dithering algorithms that I know of offered no guarantees that their ditherings were in any way near-optimal. They were justified solely by trying them on various test-images and aesthetically judging them as "working well" or "not." However, we now see that our suggested political districting algorithm is quite similar to the Witten-Neal dithering method (albeit, I think, should perform somewhat better) and it does come with optimality approximate guarantees. It also suggests that Sierpinski's or the Peano-Smith curve ought to be preferred over (what had been commonly used) Hilbert's or Peano's curves.
Suppose in Euclidean d-space, we have a connected compact measurable set C.
Definition: C is "halvable" if it can be divided into two interior-disjoint connected subsets A and B, such that both's closures are congruent (perhaps with mirroring) to 2-1/dC. C is "trisectable" if it can be divided into three interior-disjoint connected subsets, all of whose closures are congruent (perhaps with mirroring) to 3-1/dC.
Halvable objects seem of fundamental importance for anybody who wants to design nifty binary-tree subdivision-schemes for d-space; trisectable objects ditto for ternary-tree subdivisions. The aim of this section is to completely classify all halvable and trisectable objects. But we will only partly succeed.
PARALLELIPIPED EXAMPLE: A parallelipiped whose d sidelengths are in the ratio
is halvable, and trisectable if
Observation: For halvable obects, we never have to worry about congruences involving mirroring. More precisely, any halvable body C such that A and B are mirrored with respect to each other, must be mirror-symmetric. Hence A and B must either both be congruent to C, or both be congruent to the mirror image of C, or C is mirror-symmetric in which case the whole issue is moot.
TILING LEMMA: In any dimension, any convex halvable or trisectable object must be a convex polytope that tiles d-space. In the trisectable case the "tiling" may involve mirrored tiles, but in the halvable case the tiling is proper.
Proof: By splitting into two, then each of those into two, etc, we get a "binary tree" tiling with 2K tiles; then by König's infinity lemma an infinite binary tree must exist, i.e. a tiling of the entire plane; and since each tile is convex the boundaries between tiles must be straight, i.e. hyperplanes, forcing each one to be a convex polytope. By the observation above, no mirrored tiles are needed. (Similar proof for trisectable, but without the benefit of the no-mirror observation.) QED.
THEOREM (all convex halvable 2D objects): The only 2-dimensional convex halvable objects are the 45-45-90 right triangle (with sidelengths in the ratio 1:1:√2) and the parallelograms in the example above with d=2. Of these, the only ones which do not require a mirror-congruence are the 45-45-90 right triangle and the rectangle with sidelength ratio √2 (both of which are bilaterally-symmetric).
Proof: C must tile the plane (indeed, face-to-face and employing orientation-preserving congruences only). A convex tiler must be a polygon. If it is a polygon it must have ≤4 sides since you can easily see that trying to cut an n-gon into two via a line cannot yield two n-gons if n≥5.
Case I: If C is a triangle, then it cannot be obtuse because the split-line would have to cut both the obtuse angle and the longest side, in which case at least one of the child-triangles would necessarily be non-obtuse, a contradiction. C also cannot be an acute triangle, because again the split-line would have to cut the longest side, in which case at least one of the two angles it made with that side would be non-acute. Hence if C is a triangle it must be a right triangle. It then is trivial to see it must also be isoceles, forcing 45-45-90 (and that works, since bisecting the largest angle and side indeed cuts this triangle into two half-area triangles similar to the original).
Case II: If C is a 4-gon then the cut must be a line cutting both among two non-adjacent edges. C plainly cannot have two consecutive obtuse angles since that would prevent A≅B. And equivalently, C cannot have two consecutive acute angles. If the obtuse angles are nonconsecutive, then they must be equal to allow A≅B; and the two acutes must also be equal. That forces C to be a parallelogram, whereupon the only possible sidelength ratio is √2 (and that works – bisect the longest sides). QED.
At first I conjectured that there were no nonconvex halvable objects. However
THEOREM (nonconvex halvable 2D objects): At least two 2-dimensional nonconvex halvable objects (whose interiors are homeomorphic to an open ball) exist, indeed all the ones we shall construct are centrosymmetric, tile (a rotated version of) themselves via translations only, and have "fractal" boundaries.
Proof: The objects we shall construct arise from "weird binary" systems for representing complex numbers.
To review: The usual binary number system employs digit-set {0,1} and radix B=2 and (with a decimal point) can represent any nonnegative real. It obeys 1+1=102 and yields a trivial tiling of the real line by unit-length line segments. One could also consider B=–2 ("negabinary") still with digit-set {0,1}; for it we have 1+1=110-2 and 0-1=11-2 and (with a decimal point) we can now represent any real of either sign.
We shall instead consider complex radices B having |B|=√2 – albeit we shall still use the digit-set {0,1} – and choose B in such a way that we can represent (with a decimal point) any complex number. Each of these yields a tiling of the complex plane by translates of the set
where all possible choices for the ak={0 or 1} are made independently for each k. Note that T and T+1 are two interior-disjoint tiles whose union is BT (a rotated and √2-scaled version of T). The fact T tiles the plane by translation arises as in the tiling lemma above via König's infinity lemma.
|
|
|
|
|
My computer systematically searched for every possible "weird binary" system obeying either 1+1=x or 0-1=x where x is a bitstring with up to 13 bits. (These identities permit addition and subtraction.) There are no others. [Similar searches were conducted for weird ternary ... duodecimal, with the results shown in tables I.3 .. I.7.] But it remains conceivable, although unlikely, that other such systems exist, which would have been found had my computer searched sufficiently far beyond 13 bits. The question is equivalent to whether any further complex B exist satisfying both |B|=√2 and that the sum of some finite subset of the Bk for k=0,1,2,... equals 2. [For example the last line of table I.2 arises from B2+B3=2 where B=i-1.] Since for any given subset this is three real equations which need to be satisfied by only two real variables (the real and imaginary parts of B), it is a miracle whenever a solution exists. Benedek & Panzone 1997 claim to have solved this problem and proven that no further miracles occur, i.e. that the systems listed in table I.2 are the only allowed "weird binary" complex-base number systems – but I have not seen their paper and do not know the exact statement of their claim.
Anyhow, of the 4 systems tabulated in table I.2, B=i√2 leads to the boring 1×√2 rectangle as a tile (convex), but the other three each yield nonconvex tiles with fractal boundaries (albeut the two systems involving √7 in their bases both yield the same tile, up to mirroring).
| TwinDragon halvable object arising from weird binary with radix B=i-1. (Its boundary has Hausssdorf dimension≈1.523627.) | Tame TwinDragon halvable object arising from weird binary with radix B=(1+i√7)/2; dim(boundary)≈1.21076. |

|

|
|
Eisenstein quarterable object arising from weird quaternary with radix
B=–2 (Benedek & Panzone 1998).
These work even though the B=±2 weird-quaternary number systems have no nice addition formulas! | Another quarterable object from weird quaternary with radix B=2, found by Gosper. Images by Gerald A. Edgar, Wikipedia, and R.William Gosper. Each of these 4 objects tiles the plane. |

|

|
Note from its defining formula that T arising from weird binary is centrosymmetric
since {0,1} is. Let TK be the approximate version of T
got by using only the first K terms in its defining sum; this is a set with 2K
points in a bounded region, including both 0 and at least two nonzero
points within
THEOREM (halvable or trisectable objects with nice boundaries): If a 2D halvable or trisectable object has piecewise-differentiable boundary – or if its boundary has finite arc-length – then it must be convex. (Nonconvex halvable objects always have "fractal" boundaries.) Hence our above classification of convex halvable objects is really a classification of all halvable objects with well-behaved boundaries.
Proof sketch:
If the cut-curves between the pieces are anything other than a single line segment
(i.e. "bent") then by continuing the recursion
to get a tiling of our original object by 2K or 3K
copies when K→∞, we find that the cut-curve must be "infinitely wiggly,"
i.e. have essentially self-similar wiggles at every length scale, hence must
be nondifferentiable and with infinite arc-length
in essentially the same manner as the Weierstrass
nowhere-differentible Fourier series
If on the other hand the cuts all are straight, then consider the integral of the |curvature| around the boundary (which for a convex 2D object, i.e. one with everywhere-nonnegative curvature, always equals 2π, but for a nonconvex object always exceeds 2π; this integral is invariant to rescaling). Cutting necessarily increases the fraction of the boundary with curvature≥0 or decreases the value of the integral. Either contradicts the requirement that all tiles be similar to the original. QED.
THEOREM (trisectable 2D convex objects): The only convex 2-dimensional trisectable objects (or ones with finite-arc-length boundaries, see preceding theorem) are parallelograms with side-ratio √3.
Proof: Again, it is easy to see that it is impossible to divide an n-gon into three n-gons if n≥5.
A quadrilateral with two consecutive obtuse angles cannot be cut into three pieces, each similar to the original, as can be seen just by considering the one piece (that must exist) that is cut off by a single cut-line. Thus a trisectable quadrilateral must be a parallelogram. A parallelogram can be cut into three parallelograms in exactly two different ways; demanding the pieces be similar to the original forces the original sidelength ratio to be √3 and √2 respectively; but in the latter case two of the pieces are smaller than the third, so only √3 is permissible.
A triangle can be cut into three triangles in exactly three ways. Label all the angles with a,b,c in such a way that all three pieces are similar – i.e. each has angle-set {a,b,c} – and then solve the 5 or 6 angle-sum equations (one equation at each vertex of the diagram, plus the additional equation a+b+c=180) saying that the sum of the angles round a point is 360 degrees, at a halfplane is 180, and at an original angle is that angle (we also demand the original triangle have angle-set {a,b,c}). Do this exhaustively for all possible labelings and discard solutions with nonpositive angles. The result: there are no solutions (as is not surprising since usually 5 or 6 equations overdetermine 3 variables) – it is not possible to cut a triangle into three pieces, each similar to the original. (It's also possible to see this in a faster and less-brute manner; try it.) QED.
THEOREM (nonconvex 2D fractal-boundaried objects): At least two 2D nonconvex trisectable "fractal" objects exist.
Proof: These arise in a similar manner to before but now using "weird ternary" instead of "weird binary" number systems, see table I.3. All the shapes that arise are centrosymmetric because our ternary digit set {-1, 0, +1} is centrosymmetric. QED.
Remark. None of the weird binary systems in table I.2 yield new good plane-filling curves because their recursive definition diagrams all would be topologically equivalent to splitting a 1×√2 rectangle into two half-area scaled copies (in fact this is exactly what we get for radix B=i√2) whereupon there is no topologically-allowed way to "place the arrows inside the regions." Of the weird ternary systems the only one which yields a good plane-filling curve is the Peano-Smith curve (again) which arises from the only non-fractal case B=i√3 in table I.3. The reason the others do not work is that their recursive definition diagrams would involve chiral shapes with fractal-boundaries. The problem is not the fractal nature of their boundaries, the problem is their chiral mirror-nonsymmetry, i.e. the same problem that prevents a parallelogram with side-length ratio √3 from being used except in the achiral case where it is a rectangle. The Peano-Smith (s=3) curve can now be re-described in an elegant manner via the recursively-defined map t=P3(z), where z is complex represented in radix B=i√3 with all 0s to the left of the decimal point (this set is an 0-centered rectangle with area=√3), while t is real with |2t|≤√3:
where conj is the complex-conjugation operator.
So we see that even though nonconvex halvable and trisectable 2D objects exist,
Could it be, then, that the Sierpinski and Peano-Smith curves actually are the only good plane-filling curves with s=2 and s=3 respectively? No! A different halvable nonconvex object called the "Heighway dragon" was discovered in the 1960s by NASA physicist John E. Heighway by accident while repeatedly folding a strip of paper. The Heighway dragon arises in an interesting way. Recall that the usual decomposition of an isoceles right triangle into two can be got by drawing such a triangle, then rotating it +90° (the + meaning anticlockwise) about its apex to get the second triangle. If we do the same thing, but rotate +90° about one of the nonapex (45-degree) vertices to duplicate it, then rotate the resulting 2-triangle-chain object +90° about one of its 45°-end-vertices to duplicate it, then rotate the resulting 4-triangle-chain object +90°, about one of its 45°-end-vertices to duplicate that, and continue on for K stages to get a chain of 2K identical triangles (which all remain interior-disjoint!), then in the limit K→∞ we obtain a picture of the Heighway dragon. This object tiles the plane. Also two of them tile a √2-scaled copy of itself. (Also as Davis & Knuth discovered, two translated disjoint Heighway dragons tile a twindragon!) The Heighway dragon, although connected (and filled by a planefilling curve) has an interior consisting of an infinite number of disconnected components, see Ngai & Nguyen 2003. That makes it much worse-behaved than the "twindragon" and "tame twindragon" above, whose interiors each are homeomorphic to open balls.
The "Levy Dragon" by Levy 1938 (rediscovered by Gosper in 1972 under the name "C-curve") also is related to the isoceles right triangle by a related mechanism. Two copies again tile a √2-scaled version of itself, and Levy dragons tile the plane. It is even worse-behaved: Not only does the Levy dragon's interior have an infinite number of disconnected components, see Bailey, Kim, Strichartz 2002 (each component individually is well behaved and is one of a finite set of possible polygonal shapes!), but the plane-filling curve that fills it crosses itself a countably-infinite number of times (in contrast, the Heighway plane-filling curve never crosses over itself).
A different trisectable nonconvex object called the "terdragon" was found by C.Davis & D.E.Knuth in 1970. It arises as follows. Begin with a 60-120-60-120° rhombus. Rotate it +60° about a 60°-vertex and +60° about its other 60°-vertex to triplicate it. The resulting 3-rhomb object can then be triplicated again in the same fashion to get a 9-rhomb object, and so on for K stages to get a 3K-rhomb object. The set-limit as K→∞ of that (of course scaled by 3-K/2), is the terdragon.
All three are illustrated below. The terdragon yields a good plane-filling curve with s=3 different from the Peano-Smith curve, and the Heighway and Levy dragons yield good plane-filling curves with s=2 different from the Sierpinski curve (but both far worse than Sierpinski as measured by the present paper's quality measure).

THEOREM (no halvable or trisectable tetrahedra): : When d=3, neither a halvable nor a trisectable tetrahedron exists.
Proof: Refer to D.M.Y.Sommerville's 1923 classification of all tetrahedra which tile 3-space in a face-to-face manner (with gap in Sommerville's proof filled by Edmonds 2007 and as summarized concisely by Goldberg 1974), and simply note that
THEOREM (more generally, no halvable d-simplex): For any dimension d≥3 no halvable d-simplex exists.
Proof: This result was proven using eigenvalues by Matousek 2005 as corrected by Safernova & Matousek. QED.
These results indicate that there is no way to generalize the Sierpinski curve to any dimension d≥3.
CONJECTURE (Ngai, Sirvent, Veerman, Wang 2000; Smith): There are exactly 6 halvable 2D objects provided the two half-area objects are required to be properly (not mirror) similar to the original. They are tabulated below. I further conjecture that the only improperly halvable 2D objects are the parallelograms in the final row of the table.
| Object | dim(boundary) | topology(interior) | symmetry | ⇒plane-filling (s=2) curve? |
|---|---|---|---|---|
| 45-45-90 triangle | 1 | Open ball. | Bilateral. | Yes (Sierpinski; very good curve). Never crosses itself. |
| 1×√2 rectangle | 1 | Open ball. | Bilateral & centrosymmetric. | No. |
| Tame twin dragon | 1.2107605332 | Open ball. | Centrosymmetric. | No. |
| TwinDragon | 1.5236270862 | Open ball. | Centrosymmetric. | No. |
| Heighway Dragon | 1.5236270862 | Infinite # connected components. | None. | Yes (never crosses itself, but curve is not "very good"). |
| Levy Dragon | 1.9340071829 | Infinite # connected components. | Bilateral. | Yes (crosses itself infinitely many times; curve is not "very good"). Levy Dragon is connected non-simply, has infinite number of holes. |
| Parallelogram with sidelength ratio √2 | 1 | Open ball. | Centrosymmetric (improperly halvable). | No. |
Ngai et al claimed to have proven this if the 2 tiles were each only allowed to be rotated by rational (measured in degrees) angles, and also claimed that a computer search indicated irrational angles could not occur. However, Richard Kenyon claimed their proof contained a major gap. Hence I have labeled this a "conjecture." I have extended their conjecture to claim that there are no improperly-halvable 2D fractal-boundaried objects.
THEOREM: Sierpinski's (with s=2) and the Peano-Smith curve with s=3 are the only good plane-filling curves (defined at start of paper) defined via a "recursive definition diagram" involving shapes with finite arclength, and with integer scaling factors s<4. In particular they are the only "very good" plane-filling curves with real scaling factors s<4.
Proof sketch: Employ the above theorems about halvable and trisectable objects. Then realize (by exhaustive trial) that there is only one way to "draw arrows" within those objects leading to a valid recursive definition diagram, and the only parallelogram allowed is a rectangle (because otherwise, in the Peano-Smith diagram in figure 1, some arrows would have to go on the long diagonal and others on the short diagonal of the parallelogram, contradicting the demand that all be the same). QED.
CONJECTURE: Sierpinski and Peano-Smith(s=3) are the uniquely best two plane-filling curves in the sense that the squared-length expected approximation factors that result from them, are less than those arising from any other plane-filling curve.
One can also make a spacefilling "tree" rather than "curve." The most natural one seems to be this: the root of the tree is center of a 1×√2 rectangle, which is split into two half-area scaled versions of same rectangle. Join the tree root to the two child box-centers via line segments, then continue recursively. With obvious changes – use the halvable d-dimensional hyperrectangle – this also works in d dimensions.
Every point in the rectangle is a tree-leaf and no two tree line segments cross. If this is done, then
THEOREM (tree-distance upperbounds Euclidean): the Euclidean distance between any two points, is upper bounded by Cd times their distance along the tree.
Proof: We compute Cd: the maximum Euclidean distance Ed is the diameter (from one corner to an antipodal corner) of the original
hyperrectangle. We find
Meanwhile the along-tree distance from any point to any other (it does not matter what the points are provided the path passes through the tree root and the two points are tree leaves; points that are internal nodes of the tree also are representable as leaves by using a longer along-tree path) is the following constant:
Then Cd=Ed/Ad. We have C2≈0.4202659978 and when d→∞ we have Cd∼[6ln2]1/2d1/2/4. QED.
We can of course use the self-similarity property of this tree asbefore to regard it as filling all of d-space, not merely this hyperrectangle.
In the other inequality direction, the distance along the tree is upper bounded in expectation by a constant times Euclidean distance, if the tree is randomly rotated and translated???
This "tree" trick presumably yields better constants than the "curve" trick in my paper, and also works for unsquared distances... ???
Most of our approximation algorithms can be derandomized, and then will still run in polynomial time (but a larger polynomial) and will now obey a slightly worse approximation guarantee, but with 100% certainty instead of merely with some success probability.
Focus for concreteness on the sum-of-squared-hop-lengths traveling salesman problem of §7. The first derendomization idea is to realize that the space-filling curve can be regarded as an infinite recursive "tree of boxes" and its relative ordering of two points A and B can be deduced simply from which boxes A and B lie in – we can stop recursive descending into smaller and smaller boxes as soon as A and B are separate boxes. The second idea is that, once we have reached sufficiently small boxes, if A and B still are not separated, then that does not matter because A and B must be so close that any ordering will do (the TSP cost will be affected negligibly). Therefore, it suffices to employ a finite tree of boxes with, for N sites, only O(N3) boxes in all. Now, there are only a finite, indeed polynomially bounded, number of combinatorially-distinct ways to rotate, translate, and scale such a finite tree-of-boxes with respect to a given N-point set. Trying them all and using the least-cost TSP obtainable from any of them, derandomizes the algorithm.
J.S.B.Mitchell's 1999 "guillotining framework" can produce approximation algorithms for many geometry problems. In other cases it may produce an approximation algorithm but you won't know it because you are not smart enough to prove an approximation guarantee. Using the dynamic programming approach of this framework we can find, in polynomial(N) steps, the "best" ordering of N point sites in the plane (or in any fixed-dimensional space) among all possible "tree-in-order" orderings arising from all possible "guillotine tree" decompositions of the plane, with, e.g. each cell in the guillotining being a K-gon with any constant upper bound on K. (With a wide variety of possible meanings for the word "best.")
It now is immediately obvious that Sierpinski and Hilbert orderings are guillotine orderings, so Mitchell will always produce an ordering at least as good as the best Sierpinski and best Hilbert ordering. It therefore follows that Mitchell's guillotining approach yields a 6.38-factor (or better) approximation for all the problems we've discussed, and does so without needing any randomization. (However, the runtimes usually will be much larger for Mitchell's approach than with our simple sort-along-random-curve algorithm, and the algorithms will also usually be much more difficult to program.)
This was not previously known, and the reason it was not known was because it is not at all obvious how to prove approximation guarantees in Mitchell's framework – especially for cost measures based on squared distances. It's remarkable how space-filling curves, which would seem at first to have nothing to do with anything (and in particular nothing to do with Mitchell's guillotining approach), produce as a side effect, approximation guarantees for Mitchell.
1. Halvable 2D and 3D objects: Classify them all. I conjecture there is no halvable 5-faced polyhedron.
2. "Best" space-filling curves: Identify the "best" among all space-filling curves, according to our criteria or closely related ones.
3. Scale factors s for good space-filling curves: Prove the integrality conjecture that s for a good spacefilling curve, must be an integer. (A counterexample which does not quite work because it does not actually yield a plane-filling curve, is the Rauzy fractal.) Find every achievable integer.
4. "Weird" complex number systems: Are there any others beside those listed in table I?
Jin Akiyama, Hiroshi Fukuda, Hiro Ito, Gisaku Nakamura:
Infinite series of generalized Gosper space filling curves,
CJCDGCGT'05 Proceedings of the 7th China-Japan conference on Discrete geometry,
combinatorics and graph theory, 2005;
Springer Lecture Notes in Computer Science #4381 (2007) 1-9.
abstract.
Jochen Alber & Rolf Niedermeier:
On Multidimensional Curves with Hilbert Property,
Theory of Computing Systems / Mathematical Systems Theory 33,4 (2000) 295-312.
David Arthur & Sergei Vassilvitskii: k-means++: The Advantages of Careful Seeding,
Proceedings 18th annual ACM-SIAM symposium on Discrete algorithms SODA (2007) 1027-1035.
S.Bailey, T.Kim, R.Strichartz: Inside the Levy Dragon,
Amer. Mathematical Monthly 109,8 (2002) 689-703.
Agnes Benedek & Rafael Panzone:
On complex bases for number systems with the digit set {0,1}.
Proceedings of the Fourth "Dr. Antonio A. R.
Monteiro" Congress on Mathematics (Spanish, in
Univ. Nac. del Sur, Bahia Blanca, 1997) 17-32.
Agnes Benedek & Rafael Panzone:
On a number system with base -2,
Communication Academia Nacional de Ciencias de Buenos Aires
23 April 1998.
Also "On the number system (-2, {0,1,exp(2π/3),exp(4π/3)})"
was pages 41-47 in
Actas V Congreso "Dr. Antonio A. Monteiro" 1999.
Dmitris Bertsimas & Michelangelo Grigni:
Worst case examples for the space filling curve heuristic for the Euclidean
traveling salesman problem, Operations Research Letters 8,5 (1989) 241-244.
Chandler Davis & Donald E. Knuth: Number representations and complex curves I,
J.Recreational Maths 3,2 (April 1970) 66-81; and II: 3,3 (July 1970) 133-149.
Allan L. Edmonds: Sommerville's missing tetrahedra,
Discrete & Computational Geometry 37,2 (2007) 287-296 [repairs lacunae in Sommerville's
1923 proof but Sommerville is found 84 years later to have had the
right answer despite the flaw in his proof].
H.Fukuda, M.Shimizu, and G.Nakamura:
New
Gosper space filling curves,
Proceedings of the International Conference on Computer Graphics and Imaging (CGIM 2001) 34-38.
Martin Gardner: In which "monster" curves force redefinition of the word "curve,"
Scientific American 235,6 (December 1976) 124-133.
Also discussed
in Gardner's book
Penrose Tiles to Trapdoor Ciphers... and the Return of Dr. Matrix,
W.H. Freeman, New York 1989.
Michael Goldberg: Three infinite familes of tetrahedral space
fillers, J. Combinatorial Theory A 16 (1974) 348-354.
C.Gotsman & M.Lindenbaum:
On
the metric properties of discrete space-filling curves,
IEEE Trans. Image Processing, 5,5 (1996) 794-797.
Hans Hahn (published posthumously):
Geometry and Intuition –
A classical description of how 'common sense',
once accepted as a basis of physics but now rejected, is also inadequate as a
foundation for mathematics,
Scientific American 190,4 (April 1954) 84-91.
S.W.Hess, J.B.Weaver, H.J.Siegfeldt, J.N.Whelan, P.A.Zitlau:
Nonpartisan
political districting by computer, Operations Research 13,6 (1965) 998-1006.
David Hilbert: Über die stetige Abbildung einer Linie auf ein Flächenstück,
Mathematische Annalen 38,3 (1891) 459-460.
[See also Hilbert's Gesammelte Abhandlungen, Chelsea Pub. Co, Bronx NY 1965, 3 vols
QA3.H612???]
D.S.Johnson, L.A.McGeoch, E.E.Rothberg:
Asymptotic Experimental Analysis for the Held-Karp Traveling Salesman Bound,
pp. 341-350
in Proceedings of the Sixth Annual ACM-SIAM Symposium on Discrete Algorithms SODA 1996.
Tapas Kanungo, David M. Mount, Nathan S. Netanyahu, Christine D. Piatko, Ruth Silverman,
Angela Y. Wu:
A local search approximation algorithm for k-means clustering,
Comput. Geometry 28,2-3 (2004) 89-112.
Richard Kenyon & Boris Solomyak:
On the Characterization of
Expansion Maps for Self-Affine Tilings,
Discrete & Computational Geometry 43,3 (2010) 577-593.
Konrad Knopp: Einheitliche Erzeugung und Darstellung der Kurven von Peano, Osgood und von Koch,
Arch. Math. Phys. 26 (1917) 103-115.
Paul Levy:
Les courbes planes ou gauches et les surfaces composee de parties semblales au tout,
Journal de l'Ecole Polytechnique (1938), 227-247 & 249-291.
Translated into English pp.181-239 in Classics on Fractals
(Gerald A. Edgar, Editor, Addison-Wesley 1993)
titled "Plane or space curves and surfaces consisting of parts similar to the whole."
Ramgopal R. Mettu & C. Greg Plaxton:
Optimal Time Bounds for Approximate Clustering,
Machine Learning Journal 56,1/2/3 (2004) 35-60.
abstract.
Jiri Matousek: Nonexistence
of 2-reptile simplices,
Springer LNCS #3742 (2005) 151-169.
Contains an error, noticed by Zuzana Safernova, which is corrected
here.
Joseph S.B.Mitchell: Guillotine subdivisions approximate polygonal subdivisions...,
SIAM J. Computing 28,4 (1999) 1298-1309.
E.H.Moore: On certain crinkly curves, Trans. Amer. Math'l. Soc. 1,1 (1900) 72-90.
Sze-Man Ngai & Nhu Nguyen: The Heighway dragon revisited,
Discrete & Computational Geometry 29,4 (2003) 603-623.
Sze-Man Ngai, Victor F. Sirvent, J.J.P. Veerman, Yang Wang:
On 2-reptiles in the plane,
Geometriae Dedicata 82, 1-3 (2000) 325-344.
But Richard Kenyon in Mathematical Reviews MR1789066 has dismissed
this paper as containing "a major gap."
Giuseppe Peano:
Sur une courbe, qui remplit toute une aire plane,
Mathematische Annalen 36,1 (1890) 157-160.
[See also Peano's Opera Scelte, Roma: Edizioni Cremonese, 1957-59, 3 vols,
QA3.P43???]
A.G.Percus & O.C.Martin:
Finite Size and Dimensional Dependence in the Euclidean Traveling Salesman Problem,
Physical Review Letters 76 (1996) 1188-1191.
Loren K. Platzman & John J. Bartholdi III:
Spacefilling curves and the planar travelling salesman problem,
J. Association for Computing Machinery 36,4 (1989) 719-737.
G.Polya: Uber eine Peanosche Kurve,
Bulletin Acad. Sci. de Cracovie [Sci. math. et nat. Serie A] ?? (1913) 1-9.
Hans Sagan:
Space-Filling Curves,
Springer-Verlag, 1994. QA643.S12.
Hans Sagan: A geometrization of Lebesgue's space-filling curve,
The Mathematical Intelligencer 15,4 (1993) 37-43.
W.Sierpinski: Sur une nouvelle courbe qui remplit toute une aire plaine,
Bulletin Acad. Sci. de Cracovie [Sci. math. et nat. Serie A] (1912) 462-478.
D.M.Y.Sommerville: Division of space by congruent triangles and tetrahedra,
Proc. Royal Soc Edinburgh 43 (1923) 85-116;
also Proc. Edinburgh Math'l Soc. 41 (1923) 49-57.
Andrew Spann, Dan Gulotta, Daniel Kane:
Electoral
redistricting with moment of inertia and diminishing halves methods,
pp.281-300
among the missing pages 191-332 in
UMAP (undergraduate journal of maths & applications) issue 28,3 (Fall 2007).
B.Weaver & S.W.Hess:
A procedure for nonpartisan districting,
Yale Law Journal 73 (1963) 288-308.
Ian H. Witten & M.Neal:
Using Peano curves for bilevel display of continuous tone images,
IEEE Computer Graphics & Applications 2,3 (May 1982) 47-52.