Answer to Puzzle #74: How bad can "Shortest Splitline" districts be?

Puzzle

1. Suppose we have a rectangular "country" (on a flat Earth) and suppose the population distribution inside it is uniform. If we partition it into N districts using the shortest splitline algorithm, then how much worse (in terms of total length of cutting) can it be than the hypothetical optimum districting which minimizes cutting length? In particular: prove the worst (i.e. maximum) possible ratio in the limit N→∞ is K=(3^1/2+3^-1/2)/12^1/4≈1.24080647880279946525.
2. One might now boldly conjecture that the shortest splitline algorithm never produces cutlength exceeding the optimum by more than some constant factor C no matter how the initial country is shaped, and no matter how the population is distributed inside the country. Disprove that conjecture with uniform population density.
3. Also disprove the conjecture for a square-shaped country.
4. This "Approximation Conjecture" is, however, reborn if we restrict attention to convex countries with uniform population densities. (I believe in this conjecture.) Prove the shortest splitline algorithm applied to a convex country will only employ all-internal splitlines, and will only produce convex districts.
5. Prove the Approximation Conjecture with C=K for rectangular countries with uniform population density in the N→∞ limit.
6. Prove the Approximation Conjecture in the case of convex planar countries with arbitrary smooth population densities which are everywhere bounded below and above by positive constants, in the N→∞ limit.

Answers

a. Let F(N) denote the worst (greatest) possible ratio of splitline-length to optimum cut-length. We know from Baumann's conjectured optimal configurations for N=1,2,3,4,5,6 when the rectangle is a square (see also our puzzle 66) that F(1)=F(2)=1, F(3)≥1.0265, F(4)≥1.0124, F(5)≥1.0391, and F(6)≥1.0175. Also, Baumann's min-cut-length partition of a unit-side regular hexagon into 4 equal-area pieces (puzzle 66) has length 2√3 whereas the shortest-splitline algorithm produces length 2+√3, for a cut-length-ratio of 1.07735, and Baumann's partition of a unit-side equilateral triangle into two pieces by using a circular arc has cut-length (3π√3)^1/2/6≈0.67338684 (whereas splitlining gives cut length 1/√2) for ratio 1.050075.

In the limit N→∞ we shall now demonstrate that limsup F(N)≥(3^1/2+3^-1/2)/12^1/4≈1.24086. To see this, consider a square being divided into N=3·4^k pieces. The result with shortest splitline algorithm is a grid consisting of identical rectangles each with the proportions 3×1. The half-perimeter of such a rectangle with unit area is 3^1/2+3^-1/2. Meanwhile the optimum partitioning is known by a result of Thomas C. Hales to be asymptotically the same length as the regular-hexagon "honeycomb," and note a unit-area regular hexagon has half-perimeter 12^1/4. (We did not actually need Hales's result, we merely need the trivially easier result that the honeycomb upper bounds the optimum.) Q.E.D.

We can also show liminf F(N)≥2/12^1/4≈1.0745699 by noting that no matter what N is (power of 2, or not) the final rectangles will always have perimeter at least as large as a square with the same area. (Which follows from the fact L+W is minimized with LW=1 and L,W>0 when L=W=1.)

In the same limit we now shall demonstrate the matching upper bound limsup F(N)≤(3^1/2+3^-1/2)/12^1/4≈1.24081, thus demonstrating equality – we know the limsup's exact value. This will solve problem e. Suppose we have an A×B rectangle, A≥B. (We say its "aspect ratio" is A/B.) The shortest splitline will have length B and the new two rectangles will each have aspect ratios 2B/A if N is even and if 2B>A. Even in the worst case where N=3, the aspect ratios will be 3B/A and 3B/(2A). The point of this is that

1. If we are exactly bisecting area each time then the aspect ratio, once it becomes ≤2 can never rise above 2, no matter how many further bisections occur to that rectangle.
2. Even if not, then still we can conclude that the aspect ratio, once it becomes ≤3 can never rise above 3, no matter how many further bisections occur to that rectangle.
3. The aspect ratio will get below 3 if N is large enough (in fact, if 3N>a where a is the aspect ratio).

In view of the second and third points, the final splitline districting will consist entirely of equal-area rectangles, all with aspect ratio≤3, in the N→∞ limit; this in combination with Hales's honeycomb-optimality theorem implies our upper bound.

I conjecture this limit-constant 1.2408 works not only for rectangular countries but in fact for every convex country-shape. (The intuition behind the conjecture is that in the N→∞ limit, splitlined districts will almost all be almost-rectangular.)

b. A country consisting of three equal-area blobs joined by a "Y" of thin filaments, is a counterexample. Another is:

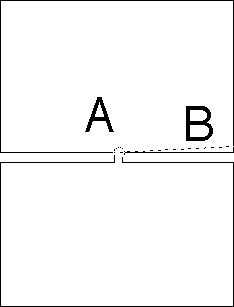
The country (shaped like two rectangles of slightly-unequal size joined by a short thin neck) can be divided in half by either (A) a short circular arc, or (B) a much longer line segment.

c. A square country with a high-population-density city near the midpoint of its East edge, and low-density rural everywhere else (total rural≈total urban population), is a counterexample with N=2. A tiny semicircle chopping off the city (or a tiny circle, if the city instead is located internally) has far smaller cutlength than the shortest splitline.

d. Splitlines are all-internal for a convex country by the definition of convexity and the inductive production of convex hemi-countries in all such splits.

f. Define the "aspect ratio" of a convex plane region R to be its diameter D (furthest point-pair separation) divided by its width W (minimum separation between two parallel lines enclosing R). The shortest splitline for any given population ratio always has length≤W. It is not hard to see that once our convex region has aspect ratio≤C, for some appropriate constant C depending roughly linearly on the ratio of upper to lower bounds for the allowed-population-density window, then it will never rise above C no matter how much further splitting is done to it. This aspect ratio bound in turn may be used to see that the Approximation Conjecture is true (again for some ratio-constant) in the N→∞ limit.

Other remarks. Raphfrk points out this lower bound

One can argue that the shortest curve-length L cutting a convex area=A width=W body into two parts while exactly bisecting area, obeys

For an equilateral triangle with SideLength=1, Baumann's optimal cut (via an arc) into two pieces has cut length √(3π√3)/6≈ 0.6733868440 whereas the shortest splitline algorithm produces a cut-line with length 1/√2≈0.7071067812 for an approximation ratio of about 1.050075. One perhaps could prove the N=2 uniform case has this approximation ratio in the worst case?

For an equilateral triangle with SideLength=1, the optimal cut (via three line segments) into three pieces has cut length (√3)/2≈0.8660254040 whereas the shortest splitline algorithm produces cut-length (5√3 - 3)/6≈0.9433756730, for an approximation ratio of about 1.089316. Perhaps this too is the worst possible ratio when N=3?

The shortest splitline sliceup of an equilateral triangle into N=4 equiareal pieces has length (1+√3+√2)/2 + (√6)/4 ≈ 1.460759749 as opposed to the conjectured minimal-length splitup (by J.Hall & E.Baumann) with cut-length≈1.305113032, for ratio≈1.119259185. [This is the greatest ratio I currently know for any convex shape with N≤6.]

A.Heppes remarked the following. If you decompose the surface of a sphere into N equal-area regions for any N>0 with N≠{2,3,4,6,12}, then the shortest net that does the job necessarily contains a nonconvex cell (because it will have a circular arc as part of its boundary).

Return to puzzles

Return to main page