Suppose you have N items from an ordered set. In one "step" you can ask "is A<B or not?" and be answered. What is the minimum number of steps to sort the items into order? To find the median item? (If N is even, then for our purposes here "median" shall mean "the lesser of the two medians.") Solve this for N=1,2,3,...,13.
A. (Worst case)
N 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
median 0 1 3 4 6 8 10 12 14 16 18 20 23 24-25 24-28
sorting 0 1 3 5 7 10 13 16 19 22 26 30 34 38 42 45-46
sortnet 0 1 3 5 9 12 16 19
Medians: Donald E. Knuth [5.3.2 of his book The Art of Computer Programming vol. III] found our table for N≤10, which was expanded to cover all N≤13 by computer search by Kenneth Oksanen. An optimal median-of-five algorithm is explained in this graphic (apparently by William Wu; "step 1" is to compare D,E, then compare A,B, then compare the two mins):
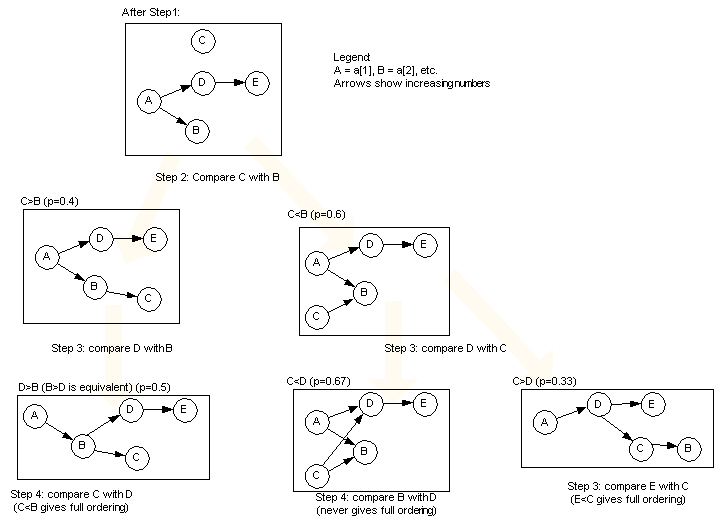
For (lower)median-of-4 compare A,B, compare C,D, compare mins, and then 1 more comparison suffices.
Sorting: The "merge insertion" sorting algorithm discovered by Lester Ford Jr. & Selmer Johnson in 1959 (also explained in 5.3.1 of Knuth's book) is now known to have worst-case optimal comparison counts for each N≤13 although it is known not to be optimal when N=47 and 52 (since better algorithms are known in those two cases). Optimality for N≤11 is trivial because for those N the information-theoretic lower bound ⌈log2N!⌉ exactly equals the Ford-Johnson comparison count. (This exact equality also holds when N=20 and N=21.) A computer search by Wells in the mid-1960s proved optimality when N=12, and searches by Peczarski proved it when N=13, 14, 15 and 22. (Peczarski estimates that a few more years of computing will probably settle the case N=16.)
L.R.Ford Jr. & S.B.Johnson: A tournament problem, Amer. Math'l Monthly 66,5 (1959) 387-389.
D.E.Knuth & E.B.Kaehler: An experiment in optimal sorting, Information Processing Letters 1 (1972) 173-176.
Mark B. Wells: Elements of Combinatorial Computing, Pergamon Press 1971.
Marcin Peczarski: New results in minimum-comparison sorting, Algorithmica 40,2 (2004) 19-37. [Optimality for N=13 was also shown by T.Kasai, S.Sawato, S.Iwata in 1994.]
Marcin Peczarski: The Ford-Johnson Algorithm Still Unbeaten for less than 47 Elements, Information Processing Letters 101,3 (2007) 126-128.
Sortnet: A special restricted "oblivious" kind of sorting algorithm, called a "sorting network," is discussed by Knuth 5.3.4; he also discusses "selection networks."
B. This average-case question is much more difficult, but it turns out (Knuth 5.3.1) that for N≤5 (but not for N=6 and 7) merge-insertion also is optimal in the expectation sense. The median-finding methods we gave above also seem optimal in the expectation sense when N≤5. [Knuth says that Y.Cesari found average-case optimal sorting methods when N=9 and N=10.]
N 1 2 3 4 5 9 10
median 0 1 2.667 4 6
sorting 0 1 2.667 4.667 6.933 18.555203 21.844162
For 3 elements, "sorting" and "median finding" are the same task. After comparing A,B(say A<B), we compare B,C. With probability=1/3 we find B<C and are done; but with probability=2/3 we find C<B and need to compare A,C (and then really are done). Thus the expected number of comparisons needed is 8/3≈2.667.
Optimum algorithms usually seem very complicated since they involve a tremendous number of cases. In practice, most people skilled in the art use non-optimal algorithms which can be proved to be optimal to within a constant factor.